
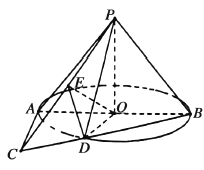
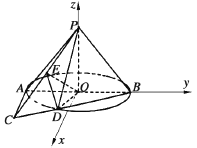
【題目】如圖,在以![]() 為頂點,母線長為
為頂點,母線長為![]() 的圓錐中,底面圓
的圓錐中,底面圓![]() 的直徑
的直徑![]() 長為2,
長為2,![]() 是圓
是圓![]() 所在平面內一點,且
所在平面內一點,且![]() 是圓
是圓![]() 的切線,連接
的切線,連接![]() 交圓
交圓![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,連接
的中點,連接![]() ,
,![]() ,當二面角
,當二面角![]() 的大小為
的大小為![]() 時,求平面
時,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)由![]() 是圓
是圓![]() 的直徑,
的直徑,![]() 與圓
與圓![]() 切于點
切于點![]() ,可得
,可得![]() ,
,
由![]() 底面圓
底面圓![]() ,可得
,可得![]() ,利用線面垂直的判定定理可知,
,利用線面垂直的判定定理可知,![]() 平面
平面![]() ,即可推出
,即可推出![]() .又在
.又在![]() 中,
中,![]() ,可推出
,可推出![]() ,利用線面垂直的判定定理可證
,利用線面垂直的判定定理可證![]() 平面
平面![]() ,從而利用面面垂直的判定定理可證出平面
,從而利用面面垂直的判定定理可證出平面![]() 平面
平面![]() .
.
(2)由![]() ,
,![]() ,可知
,可知![]() 為二面角
為二面角![]() 的平面角,
的平面角,
即![]() ,建立空間直角坐標系,易知
,建立空間直角坐標系,易知![]() ,
,
求得點的坐標如下;![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
設平面![]() 的法向量為
的法向量為![]() ,
,
![]() ,
,![]() ,
,
通過![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
可求出平面![]() 的一個法向量為
的一個法向量為![]() ,
,
∴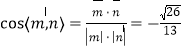 .
.
∴ 平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.
解:(1)![]() 是圓
是圓![]() 的直徑,
的直徑,![]() 與圓
與圓![]() 切于點
切于點![]() ,
,![]()
![]() 底面圓
底面圓![]() ,∴
,∴![]()
![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵在![]() 中,
中,![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() 平面
平面![]() ,從而平面
,從而平面![]() 平面
平面![]() .
.
(2)∵ ![]() ,
,![]() ,∴
,∴![]() 為二面角
為二面角![]() 的平面角,
的平面角,
∴ ![]() ,
,
如圖建立空間直角坐標系,易知![]() ,
,
則![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
設平面![]() 的法向量為
的法向量為![]() ,
,
![]() ,
,![]() ,
,
∵ ![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴ 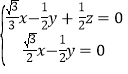 ,即
,即![]()
故平面![]() 的一個法向量為
的一個法向量為![]() ,
,
∴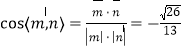 .
.
∴ 平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,PA⊥底面ABC,AC⊥BC,H為PC的中點,M為AH中點,PA=AC=2,BC=1.
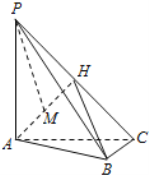
(Ⅰ)求證:AH⊥平面PBC;
(Ⅱ)求PM與平面AHB成角的正弦值;
(Ⅲ)在線段PB上是否存在點N,使得MN∥平面ABC,若存在,請說明點N的位置,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型工廠有![]() 臺大型機器,在
臺大型機器,在![]() 個月中,
個月中,![]() 臺機器至多出現
臺機器至多出現![]() 次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需
次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需![]() 名工人進行維修.每臺機器出現故障的概率為
名工人進行維修.每臺機器出現故障的概率為![]() .已知
.已知![]() 名工人每月只有維修
名工人每月只有維修![]() 臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得
臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得![]() 萬元的利潤,否則將虧損
萬元的利潤,否則將虧損![]() 萬元.該工廠每月需支付給每名維修工人
萬元.該工廠每月需支付給每名維修工人![]() 萬元的工資.
萬元的工資.
(1)若每臺機器在當月不出現故障或出現故障時有工人進行維修,則稱工廠能正常運行.若該廠只有![]() 名維修工人,求工廠每月能正常運行的概率;
名維修工人,求工廠每月能正常運行的概率;
(2)已知該廠現有![]() 名維修工人.
名維修工人.
(ⅰ)記該廠每月獲利為![]() 萬元,求
萬元,求![]() 的分布列與數學期望;
的分布列與數學期望;
(ⅱ)以工廠每月獲利的數學期望為決策依據,試問該廠是否應再招聘![]() 名維修工人?
名維修工人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的個數是( )
①一組數據的標準差越大,則說明這組數據越集中;
②曲線![]() 與曲線
與曲線![]() 的焦距相等;
的焦距相等;
③在頻率分布直方圖中,估計的中位數左邊和右邊的直方圖的面積相等;
④已知橢圓![]() ,過點
,過點![]() 作直線,當直線斜率為
作直線,當直線斜率為![]() 時,M剛好是直線被橢圓截得的弦AB的中點.
時,M剛好是直線被橢圓截得的弦AB的中點.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究高中學生對鄉村音樂的態度(喜歡和不喜歡兩種態度)與性別的關系,運用2×2列聯表進行獨立性檢驗,經計算K2=8.01,附表如下:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
參照附表,得到的正確的結論是( )
A. 有99%以上的把握認為“喜歡鄉村音樂與性別有關”
B. 有99%以上的把握認為“喜歡鄉村音樂與性別無關”
C. 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡鄉村音樂與性別有關”
D. 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡鄉村音樂與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的方程為
的方程為![]() .
.
(1)以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,求曲線
軸的正半軸為極軸建立極坐標系,求曲線![]() 的極坐標方程和直線
的極坐標方程和直線![]() 的極坐標方程;
的極坐標方程;
(2)在(1)的條件下,直線![]() 的極坐標方程為
的極坐標方程為![]() ,設曲線
,設曲線![]() 與直線
與直線![]() 的交于點
的交于點![]() 和點
和點![]() ,曲線
,曲線![]() 與直線
與直線![]() 的交于點
的交于點![]() 和點
和點![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com