
【題目】如圖,等腰直角三角形ABC所在的平面與半圓弧AB所在的平面垂直,AC⊥AB,P是弧AB上一點,且∠PAB=30°.
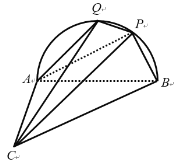
(1)證明:平面BCP⊥平面ACP;
(2)若Q是弧AP上異于AP的一個動點,當三棱錐C-APQ體積最大時,求二面角A-PQ-C的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)根據等腰直角三角形ABC所在的平面與半圓弧AB所在的平面垂直,AC⊥AB,得到![]() 平面APB,從而
平面APB,從而![]() ,又
,又![]() ,由線面垂直的判定定理得到
,由線面垂直的判定定理得到![]() 平面ACP,再由面面垂直的判定定理證明.
平面ACP,再由面面垂直的判定定理證明.
(2)由(1)知![]() 平面APB,若三棱錐C-APQ體積最大,則三角形APQ面積最大,此時
平面APB,若三棱錐C-APQ體積最大,則三角形APQ面積最大,此時![]() 為
為![]() 的中點,過點A作
的中點,過點A作![]() ,連接
,連接![]() ,得到
,得到![]() 平面ACE,從而
平面ACE,從而![]() 為二面角A-PQ-C的平面角,根據∠PAB=30°,設AC=2,求得AE,CE即可.
為二面角A-PQ-C的平面角,根據∠PAB=30°,設AC=2,求得AE,CE即可.
(1)因為等腰直角三角形ABC所在的平面與半圓弧AB所在的平面垂直,AC⊥AB,
所以![]() 平面APB,又PB
平面APB,又PB![]() 平面APB,
平面APB,
所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面ACP,又
平面ACP,又![]() 平面BCP,
平面BCP,
所以平面BCP⊥平面ACP;
(2)由(1)知![]() 平面APB,
平面APB,
所以AC為三棱錐C-APQ的高,設![]()
若三棱錐C-APQ體積最大,則三角形APQ面積最大
當![]() 為
為![]() 的中點時,三角形APQ面積最大,
的中點時,三角形APQ面積最大,
如圖所示:
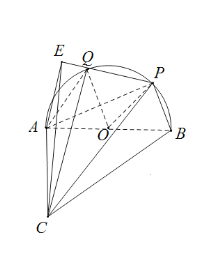
過點A作![]() ,連接
,連接![]() ,
,
所以![]() 平面ACE,
平面ACE,
所以![]() 為二面角A-PQ-C的平面角,
為二面角A-PQ-C的平面角,
因為∠PAB=30°.
所以![]() ,
,
所以![]() ,
,![]()
所以![]() ,
,
所以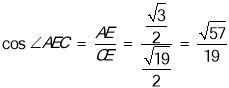 .
.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源: 題型:
【題目】動圓![]() 過定點
過定點![]() ,且在
,且在![]() 軸上截得的弦
軸上截得的弦![]() 的長為4.
的長為4.
(1)若動圓圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(2)在曲線![]() 的對稱軸上是否存在點
的對稱軸上是否存在點![]() ,使過點
,使過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 的交點
的交點![]() 滿足
滿足![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 的坐標及定值;若不存在,請說明理由.
的坐標及定值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年以來,世界經濟和貿易增長放緩,中美經貿摩擦影響持續顯現,我國對外貿易仍然表現出很強的韌性.今年以來,商務部會同各省市全面貫徹落實穩外貿決策部署,出臺了一系列政策舉措,全力營造法治化國際化便利化的營商環境,不斷提高貿易便利化水平,外貿穩規模提質量轉動力取得階段性成效,進出口保持穩中提質的發展勢頭,如圖是某省近五年進出口情況統計圖,下列描述錯誤的是( )
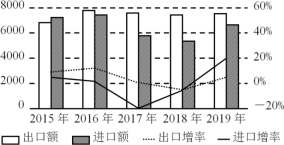
A.這五年,2015年出口額最少B.這五年,出口總額比進口總額多
C.這五年,出口增速前四年逐年下降D.這五年,2019年進口增速最快
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 上的點到點
上的點到點![]() 的距離比到直線
的距離比到直線![]() 的距離小
的距離小![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)過點![]() 且傾斜角為
且傾斜角為![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 的面積;
的面積;
(2)設![]() 為曲線
為曲線![]() 上任意一點,點
上任意一點,點![]() ,是否存在垂直于
,是否存在垂直于![]() 軸的直線
軸的直線![]() ,使得
,使得![]() 被以
被以![]() 為直徑的圓截得的弦長恒為定值?若存在,求出
為直徑的圓截得的弦長恒為定值?若存在,求出![]() 的方程和定值;若不存在,說明理由.
的方程和定值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若曲線![]() 在點(1,0)處的切線為l : x+y-1=0,求a,b的值;
在點(1,0)處的切線為l : x+y-1=0,求a,b的值;
(3)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com