【題目】如圖，在平面直角坐標系
中，點
，直線
，設圓
的半徑為1， 圓心在
上.
（1）若圓心也在直線
上，過點
作圓的切線，求切線方程；
（2）若圓上存在點
，使
，求圓心的橫坐標
的取值范圍.
【答案】（1）
或
（2）
【解析】
試題分析：（1）兩直線方程聯立可解得圓心坐標，又知圓
的半徑為
，可得圓的方程，根據點到直線距離公式，列方程可求得直線斜率，進而得切線方程；（2）根據圓的圓心在直線
：
上可設圓的方程為
，由
可得
的軌跡方程為
，若圓上存在點，使，只需兩圓有公共點即可.
試題解析：（1）由
得圓心
，
∵圓的半徑為1，
∴圓的方程為：
，
顯然切線的斜率一定存在，設所求圓的切線方程為
，即
．
∴
，
∴
，∴
或
．
∴所求圓的切線方程為或．
（2）∵圓的圓心在直線：上，所以，設圓心為
，
則圓的方程為．
又∵，
∴設為
，則
，整理得，設為圓
．
所以點應該既在圓上又在圓上，即圓和圓有交點，
∴
，
由
，得
，
由
，得
．
綜上所述，
的取值范圍為．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知等差數列{an}和等比數列{bn}滿足a1=b1=1，a2+a4=10，b2b4=a5 ．
（Ⅰ）求{an}的通項公式；
（Ⅱ）求和：b1+b3+b5+…+b2n﹣1 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如圖,以C為原點,分別以CA,CB,CC1為x,y,z軸建立空間直角坐標系.
(1)求平面A1B1C的法向量;
(2)求直線AC與平面A1B1C夾角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列關于概率和統計的幾種說法：
①10名工人某天生產同一種零件，生產的件數分別是15，17，14，10，15，17，17，16，14，12，設其平均數為a，中位數為b，眾數為c，則a，b，c的大小關系為c＞a＞b；
②樣本4，2，1，0，－2的標準差是2；
③在面積為S的△ABC內任選一點P，則隨機事件“△PBC的面積小于
”的概率為
；
④從寫有0，1，2，…，9的十張卡片中，有放回地每次抽一張，連抽兩次，則兩張卡片上的數字各不相同的概率是
.
其中正確說法的序號有________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,在底面為平行四邊形的四棱錐O-ABCD中,BC⊥平面OAB,E為OB中點,OA=AD=2AB=2,OB=
.
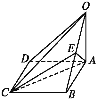
(1)求證:平面OAD⊥平面ABCD;
(2)求二面角B-AC-E的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a,b為異面直線，且所成的角為70°，過空間一點作直線l，直線l與a,b均異面，且所成的角均為50°，則滿足條件的直線共有( ) 條
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】△ABC的內角A，B，C的對邊分別為a，b，c，已知△ABC的面積為 
．（12分）
（1）求sinBsinC；
（2）若6cosBcosC=1，a=3，求△ABC的周長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
