
【題目】某書店剛剛上市了《中國古代數(shù)學(xué)史》,銷售前該書店擬定了5種單價(jià)進(jìn)行試銷,每種單價(jià)(![]() 元)試銷l天,得到如表單價(jià)
元)試銷l天,得到如表單價(jià)![]() (元)與銷量
(元)與銷量![]() (冊)數(shù)據(jù):
(冊)數(shù)據(jù):
單價(jià) | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
(l)根據(jù)表中數(shù)據(jù),請建立![]() 關(guān)于
關(guān)于![]() 的回歸直線方程:
的回歸直線方程:
(2)預(yù)計(jì)今后的銷售中,銷量![]() (冊)與單價(jià)
(冊)與單價(jià)![]() (元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價(jià)應(yīng)定為多少元?
(元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價(jià)應(yīng)定為多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A.命題“?x∈R,2x>0”的否定是“?x0∈R,2 ![]() <0”
<0”
B.命題“若sinx=siny,則x=y”的逆否命題為真命題
C.若命題p,¬q都是真命題,則命題“p∧q”為真命題
D.命題“若△ABC為銳角三角形,則有sinA>cosB”是真命題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高校從參加今年自主招生考試的學(xué)生中隨機(jī)抽取容量為![]() 的學(xué)生成績樣本,得頻率分布表如下:
的學(xué)生成績樣本,得頻率分布表如下:
組號 | 分組 | 頻率 | 頻數(shù) |
第一組 |
|
|
|
第二組 |
| ① |
|
第三組 |
|
| ② |
第四組 |
|
|
|
第五組 |
|
|
|
合計(jì) |
|
| |
(1)寫出表中①、②位置的數(shù)據(jù);
(2)估計(jì)成績不低于![]() 分的學(xué)生約占多少;
分的學(xué)生約占多少;
(3)為了選拔出更優(yōu)秀的學(xué)生,高校決定在第三、四、五組中用分層抽樣法抽取![]() 名學(xué)生進(jìn)行第二輪考核,分別求第三、四、五各組參加考核的人數(shù).
名學(xué)生進(jìn)行第二輪考核,分別求第三、四、五各組參加考核的人數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形![]() 中
中![]() ,E為
,E為![]() 的中點(diǎn),將
的中點(diǎn),將![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,
的位置,![]() 平面
平面![]() ,
,![]() 為
為![]() 的中點(diǎn),則在翻折過程中,下列結(jié)論正確的是( )
的中點(diǎn),則在翻折過程中,下列結(jié)論正確的是( )
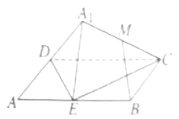
A.恒有![]() 平面
平面![]()
B.B與M兩點(diǎn)間距離恒為定值
C.三棱錐![]() 的體積的最大值為
的體積的最大值為![]()
D.存在某個(gè)位置,使得平面![]() ⊥平面
⊥平面![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數(shù)![]() .
.
(1)解不等式:![]() ;
;
(2)對任意![]() ,
,![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() ,
,![]() 中點(diǎn),
中點(diǎn),![]() ,
,![]() .現(xiàn)將
.現(xiàn)將![]() 沿
沿![]() 折起,如圖2所示,使二面角
折起,如圖2所示,使二面角![]() 為
為![]() ,
,![]() 是
是![]() 的中點(diǎn).
的中點(diǎn).
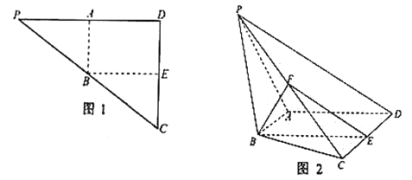
(1)求證:面![]() 面
面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
已知![]() 是遞增數(shù)列,其前
是遞增數(shù)列,其前![]() 項(xiàng)和為
項(xiàng)和為![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求數(shù)列![]() 的通項(xiàng)
的通項(xiàng)![]() ;
;
(Ⅱ)是否存在![]() 使得
使得![]() 成立?若存在,寫出一組符合條件的
成立?若存在,寫出一組符合條件的![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(Ⅲ)設(shè)![]() ,若對于任意的
,若對于任意的![]() ,不等式
,不等式
![]() 恒成立,求正整數(shù)
恒成立,求正整數(shù)![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4﹣4:極坐標(biāo)與參數(shù)方程
極坐標(biāo)系與直角坐標(biāo)系xOy有相同的長度單位,以原點(diǎn)O為極點(diǎn),以x軸正半軸為極軸.已知曲線C1的極坐標(biāo)方程為 ![]() ,曲線C2的極坐標(biāo)方程為ρsinθ=a(a>0),射線
,曲線C2的極坐標(biāo)方程為ρsinθ=a(a>0),射線 ![]() ,
, ![]() 與曲線C1分別交異于極點(diǎn)O的四點(diǎn)A,B,C,D.
與曲線C1分別交異于極點(diǎn)O的四點(diǎn)A,B,C,D.
(Ⅰ)若曲線C1關(guān)于曲線C2對稱,求a的值,并把曲線C1和C2化成直角坐標(biāo)方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com