
【題目】某大學生在開學季準備銷售一種文具盒進行試創(chuàng)業(yè),在一個開學季內,每售出1盒該產品獲利潤50元,未售出的產品,每盒虧損30元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了160盒該產品,以![]() (單位:盒,
(單位:盒,![]() )表示這個開學季內的市場需求量,
)表示這個開學季內的市場需求量,![]() (單位:元)表示這個開學季內經銷該產品的利潤.
(單位:元)表示這個開學季內經銷該產品的利潤.
(1)根據直方圖估計這個開學季內市場需求量![]() 和中位數;
和中位數;
(2)將![]() 表示為
表示為![]() 的函數;
的函數;
(3)根據直方圖估計利潤![]() 不少于4800元的概率
不少于4800元的概率
科目:高中數學 來源: 題型:
【題目】如圖,直角梯形![]() 與等腰直角三角形
與等腰直角三角形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() .
.

(1)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為及時了解適齡公務員對開放生育二胎政策的態(tài)度,某部門隨機調查了90位30歲到40歲的公務員,得到情況如下表:
(1)判斷是否有99%以上的把握認為“生二胎意愿與性別有關”,并說明理由;
(2)現把以上頻率當作概率,若從社會上隨機獨立抽取三位30歲到40歲的男公務員訪問,求這三人中至少有一人有意愿生二胎的概率.
(3)已知15位有意愿生二胎的女性公務員中有兩位來自省婦聯(lián),該部門打算從這15位有意愿生二胎的女性公務員中隨機邀請兩位來參加座談,設邀請的2人中來自省女聯(lián)的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
男性公務員 | 女性公務員 | 總計 | |
有意愿生二胎 | 30 | 15 | 45 |
無意愿生二胎 | 20 | 25 | 45 |
總計 | 50 | 40 | 90 |
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知矩形![]() ,將
,將![]() 沿矩形的對角線
沿矩形的對角線![]() 所在的直線進行翻折,在翻折過程中 ( )
所在的直線進行翻折,在翻折過程中 ( )
A. 存在某個位置,使得直線![]() 與直線
與直線![]() 垂直
垂直
B. 存在某個位置,使得直線![]() 與直線
與直線![]() 垂直
垂直
C. 存在某個位置,使得直線![]() 與直線
與直線![]() 垂直
垂直
D. 對任意位置,三對直線“![]() 與
與![]() ”,“
”,“![]() 與
與![]() ”,“
”,“![]() 與
與![]() ”均不垂直
”均不垂直
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2-2x+1.
(1)當![]() ,試討論函數f(x)的單調性;
,試討論函數f(x)的單調性;
(2)若![]() ≤a≤1,且f(x)在[1,3]上的最大值為M(a),最小值為N(a),令g(a)=M(a)-N(a),求g(a)的表達式;
≤a≤1,且f(x)在[1,3]上的最大值為M(a),最小值為N(a),令g(a)=M(a)-N(a),求g(a)的表達式;
(3)在(2)的條件下,求g(a)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了了解全校學生的上網情況,在全校采用隨機抽樣的方法抽取了40名學生(其中男女生人數恰好各占一半)進行問卷調查,并進行了統(tǒng)計,按男女分為兩組,再將每組學生的月上網次數分為5組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如圖所示的頻率分布直方圖:
,得到如圖所示的頻率分布直方圖:
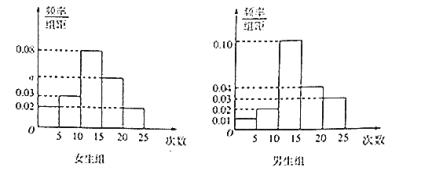
(Ⅰ)寫出![]() 的值;
的值;
(Ⅱ)在抽取的40名學生中,從月上網次數不少于20次的學生中隨機抽取3人 ,并用![]() 表示其中男生的人數,求
表示其中男生的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4.
的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 是橢圓
是橢圓![]() 的左頂點,經過左焦點
的左頂點,經過左焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 與
與![]() 的面積之差的絕對值的最大值.(
的面積之差的絕對值的最大值.(![]() 為坐標原點)
為坐標原點)
查看答案和解析>>
科目:高中數學 來源: 題型:
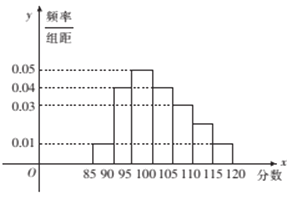
【題目】某校高二奧賽班![]() 名學生的物理測評成績(滿分120分)分布直方圖如下,已知分數在100-110的學生數有21人.
名學生的物理測評成績(滿分120分)分布直方圖如下,已知分數在100-110的學生數有21人.
(1)求總人數![]() 和分數在110-115分的人數
和分數在110-115分的人數![]() ;
;
(2)現準備從分數在110-115的![]() 名學生(女生占
名學生(女生占![]() )中任選3人,求其中恰好含有一名女生的概率;
)中任選3人,求其中恰好含有一名女生的概率;
(3)為了分析某個學生的學習狀態(tài),對其下一階段的學生提供指導性建議,對他前7次考試的數學成績![]() (滿分150分),物理成績
(滿分150分),物理成績![]() 進行分析,下面是該生7次考試的成績.
進行分析,下面是該生7次考試的成績.
數學 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知該生的物理成績![]() 與數學成績
與數學成績![]() 是線性相關的,若該生的數學成績達到130分,請你估計他的物理成績大約是多少?
是線性相關的,若該生的數學成績達到130分,請你估計他的物理成績大約是多少?
附:對于一組數據![]() ,
,![]() ……
……![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: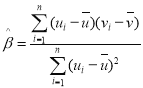 ,
,![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com