
【題目】如圖,已知矩形 ![]() 所在平面與等腰直角三角形
所在平面與等腰直角三角形 ![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
, ![]() ,
, ![]() 為線段
為線段 ![]() 的中點.
的中點.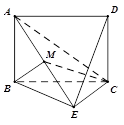
(Ⅰ)證明: ![]() ;
;
(Ⅱ)求 ![]() 與平面
與平面 ![]() 所成的角的余弦值.
所成的角的余弦值.
【答案】解:(Ⅰ) 因為 ![]() ,所以
,所以 ![]() ,故
,故 ![]() .因為
.因為 ![]() ,所以
,所以 ![]() ,故
,故 ![]() .
.
因為 ![]() ,
, ![]() 為
為 ![]() 的中點,所以
的中點,所以 ![]() .
.
所以 ![]() .
.
(Ⅱ)如圖,將幾何體 ![]() 補成三棱柱
補成三棱柱 ![]() ,
,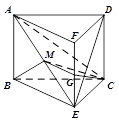
設 ![]() 的中點為
的中點為 ![]() ,連結
,連結 ![]() .
.
因為 ![]() ,所以
,所以 ![]() .
.
因此 ![]() 為
為 ![]() 與平面
與平面 ![]() 所成的角.
所成的角.
不妨設 ![]() ,則
,則 ![]() ,因此
,因此 ![]() ,
, ![]() ,
, ![]() ,故
,故 ![]() ,
,
所以 ![]() 與平面
與平面 ![]() 所成的角的余弦值為
所成的角的余弦值為 ![]() .
.
【解析】(Ⅰ)由已知推導出AB⊥EC,EC⊥BM,AE⊥BM,由此能證明BM⊥平面AEC.
(Ⅱ)將幾何體ABCDE補成三棱柱AFD-BEC,設EF的中點為G,連結MG,GC,推導出∠MCG為MC與平面DEC所成的角,由此能求出MC與平面DEC所成的角的余弦值.
【考點精析】掌握直線與平面垂直的判定是解答本題的根本,需要知道一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想.


科目:高中數學 來源: 題型:
【題目】在直角坐標系中 ![]() 中,曲線
中,曲線 ![]() 的參數方程為
的參數方程為 ![]() 為參數,
為參數, ![]() ). 以坐標原點為極點,
). 以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,已知直線
軸正半軸為極軸建立極坐標系,已知直線 ![]() 的極坐標方程為
的極坐標方程為 ![]() .
.
(1)設 ![]() 是曲線
是曲線 ![]() 上的一個動點,當
上的一個動點,當 ![]() 時,求點
時,求點 ![]() 到直線
到直線 ![]() 的距離的最大值;
的距離的最大值;
(2)若曲線 ![]() 上所有的點均在直線
上所有的點均在直線 ![]() 的右下方,求
的右下方,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在一個坡度一定的山坡AC的頂上有一高度為25m的建筑物CD,為了測量該山坡相對于水平地面的坡角θ,在山坡的A處測得∠DAC=15°,沿山坡前進50m到達B處,又測得∠DBC=45°,根據以上數據可得cosθ= . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網店和實體店各有利弊,兩者的結合將在未來一段時期內,成為商業的一個主要發展方向.某品牌行車記錄儀支架銷售公司從 ![]() 年
年 ![]() 月起開展網絡銷售與實體店體驗安裝結合的銷售模式.根據幾個月運營發現,產品的月銷量
月起開展網絡銷售與實體店體驗安裝結合的銷售模式.根據幾個月運營發現,產品的月銷量 ![]() 萬件與投入實體店體驗安裝的費用
萬件與投入實體店體驗安裝的費用 ![]() 萬元之間滿足
萬元之間滿足 ![]() 函數關系式.已知網店每月固定的各種費用支出為
函數關系式.已知網店每月固定的各種費用支出為 ![]() 萬元,產品每
萬元,產品每 ![]() 萬件進貨價格為
萬件進貨價格為 ![]() 萬元,若每件產品的售價定為“進貨價的
萬元,若每件產品的售價定為“進貨價的 ![]() ”與“平均每件產品的實體店體驗安裝費用的一半”之和,則該公司最大月利潤是萬元.
”與“平均每件產品的實體店體驗安裝費用的一半”之和,則該公司最大月利潤是萬元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ln(1+x)+mln(1-x)是偶函數,則( )
A.m=1,且f(x)在(0,1)上是增函數
B.m=1,且f(x)在(0,1)上是減函數
C.m=-1,且f(x)在(0,1)上是增函數
D.m=-1,且f(x)在(0,1)上是減函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》卷5《商功》記載一個問題“今有圓堡瑽,周四丈八尺,高一丈一尺 .問積幾何?答曰:二千一百一十二尺.術曰:周自相乘,以高乘之,十二而一”.這里所說的圓堡瑽就是圓柱體,它的體積為“周自相乘,以高乘之,十二而一”. 就是說:圓堡瑽(圓柱體)的體積為 ![]() (底面圓的周長的平方
(底面圓的周長的平方 ![]() 高),則由此可推得圓周率
高),則由此可推得圓周率 ![]() 的取值為( )
的取值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數 ![]() 的部分圖像如圖所示,將
的部分圖像如圖所示,將 ![]() 的圖象向右平移
的圖象向右平移 ![]() 個單位長度后得到函數
個單位長度后得到函數 ![]() 的圖象.
的圖象.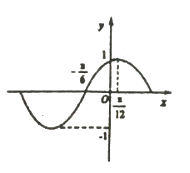
(1)求函數 ![]() 的解折式;
的解折式;
(2)在 ![]() 中,角
中,角 ![]() 滿足
滿足 ![]() ,且其外接圓的半徑
,且其外接圓的半徑 ![]() ,求
,求 ![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com