
【題目】在三棱錐![]() 中,BO、AO、CO所在直線兩兩垂直,且AO=CO,∠BAO=60°,E是AC的中點(diǎn),三棱錐
中,BO、AO、CO所在直線兩兩垂直,且AO=CO,∠BAO=60°,E是AC的中點(diǎn),三棱錐![]() 的體積為
的體積為![]()
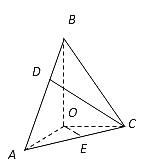
(1)求三棱錐![]() 的高;
的高;
(2)在線段AB上取一點(diǎn)D,當(dāng)D在什么位置時(shí),![]() 和
和![]() 的夾角大小為
的夾角大小為 ![]()
【答案】(1)![]() .(2)D在AB的中點(diǎn)時(shí).
.(2)D在AB的中點(diǎn)時(shí).
【解析】
(1)由題意的BO⊥平面ACO,即BO就是三棱錐B﹣ACO的高,然后根據(jù)體積建立等式關(guān)系,解之即可求出所求;
(2)以O為原點(diǎn),OA為x軸,OC為y軸,OB為z軸,建立空間直角坐標(biāo)系,設(shè)D(x,0,![]() (1﹣x)),設(shè)
(1﹣x)),設(shè)![]() 和
和![]() 的夾角為θ,則coaθ
的夾角為θ,則coaθ![]() 建立等式關(guān)系,解之即可求出x的值,從而可判定點(diǎn)D的位置.
建立等式關(guān)系,解之即可求出x的值,從而可判定點(diǎn)D的位置.
(1)由題意的BO⊥平面ACO,即BO就是三棱錐B﹣ACO的高,
在Rt△ABO中,設(shè)AO=a,∠BAO=60°,所以BO![]() a,
a,
CO=a,所以VB﹣ACO![]() AO×BO×CO
AO×BO×CO![]() a3
a3![]() .
.
所以a=1,所以三棱錐的高BO為![]() .
.
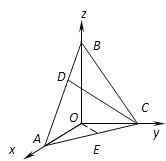
(2)以O為原點(diǎn),如圖建立空間直角坐標(biāo)系,
設(shè)D(x,0,![]() (1﹣x)),則C(0,1,0),E(
(1﹣x)),則C(0,1,0),E(![]() ,
,![]() ,0 )
,0 )
![]() (﹣x,1,
(﹣x,1,![]() ( x﹣1)),
( x﹣1)),![]() (
(![]() ,
,![]() ,0),
,0),
設(shè)![]() 和
和![]() 的夾角為θ
的夾角為θ
則coaθ![]()
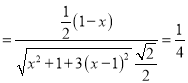 ,
,
解之得,x=2(舍去)或x![]() ,
,
所以當(dāng)D在AB的中點(diǎn)時(shí),![]() 和
和![]() 的夾角大小為arccos
的夾角大小為arccos![]() .
.


 學(xué)習(xí)實(shí)踐園地系列答案
學(xué)習(xí)實(shí)踐園地系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一次考試中,5名同學(xué)的數(shù)學(xué)、物理成績(jī)?nèi)绫硭荆?/span>
學(xué)生 |
|
|
|
|
|
數(shù)學(xué) | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
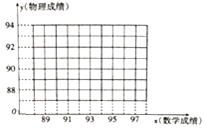
![]() 請(qǐng)?jiān)趫D中的直角坐標(biāo)系中作出這些數(shù)據(jù)的散點(diǎn)圖,并求出這些數(shù)據(jù)的回歸方程;
請(qǐng)?jiān)趫D中的直角坐標(biāo)系中作出這些數(shù)據(jù)的散點(diǎn)圖,并求出這些數(shù)據(jù)的回歸方程;
![]() 要從4名數(shù)學(xué)成績(jī)?cè)?/span>90分以上的同學(xué)中選2名參加一項(xiàng)活動(dòng),以X表示選中的同學(xué)的物理成績(jī)高于90分的人數(shù),求隨機(jī)變量X的分布列及數(shù)學(xué)期望
要從4名數(shù)學(xué)成績(jī)?cè)?/span>90分以上的同學(xué)中選2名參加一項(xiàng)活動(dòng),以X表示選中的同學(xué)的物理成績(jī)高于90分的人數(shù),求隨機(jī)變量X的分布列及數(shù)學(xué)期望![]() .
.
參考公式:線性回歸方程![]() ;,其中
;,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過拋物線![]() 焦點(diǎn)的直線
焦點(diǎn)的直線![]() 與拋物線交于
與拋物線交于![]() 、
、![]() 兩點(diǎn),與圓
兩點(diǎn),與圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),若有三條直線滿足
兩點(diǎn),若有三條直線滿足![]() ,則
,則![]() 的取值范圍為______.
的取值范圍為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中國(guó)北京世界園藝博覽會(huì)期間,某工廠生產(chǎn)
中國(guó)北京世界園藝博覽會(huì)期間,某工廠生產(chǎn)![]() 、
、![]() 、
、![]() 三種紀(jì)念品,每一種紀(jì)念品均有精品型和普通型兩種,某一天產(chǎn)量如下表:(單位:個(gè))
三種紀(jì)念品,每一種紀(jì)念品均有精品型和普通型兩種,某一天產(chǎn)量如下表:(單位:個(gè))
紀(jì)念品 | 紀(jì)念品 | 紀(jì)念品 | |
精品型 |
|
|
|
普通型 |
|
|
|
現(xiàn)采用分層抽樣的方法在這一天生產(chǎn)的紀(jì)念品中抽取![]() 個(gè),其中
個(gè),其中![]() 種紀(jì)念品有
種紀(jì)念品有![]() 個(gè).
個(gè).
(1)求![]() 的值;
的值;
()從![]() 種精品型紀(jì)念品中抽取
種精品型紀(jì)念品中抽取![]() 個(gè),其某種指標(biāo)的數(shù)據(jù)分別如下:
個(gè),其某種指標(biāo)的數(shù)據(jù)分別如下:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,把這
,把這![]() 個(gè)數(shù)據(jù)看作一個(gè)總體,其均值為
個(gè)數(shù)據(jù)看作一個(gè)總體,其均值為![]() ,方差為
,方差為![]() ,求
,求![]() 的值;
的值;
(3)用分層抽樣的方法在![]() 種紀(jì)念品中抽取一個(gè)容量為
種紀(jì)念品中抽取一個(gè)容量為![]() 的樣木,從樣本中任取
的樣木,從樣本中任取![]() 個(gè)紀(jì)念品,求至少有
個(gè)紀(jì)念品,求至少有![]() 個(gè)精品型紀(jì)念品的概率.
個(gè)精品型紀(jì)念品的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() ⊥平面
⊥平面![]() 垂足為
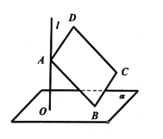
垂足為![]() 在矩形ABCD中,AD=1,AB=2,若點(diǎn)A在
在矩形ABCD中,AD=1,AB=2,若點(diǎn)A在![]() 上移動(dòng),點(diǎn)B在平面
上移動(dòng),點(diǎn)B在平面![]() 上移動(dòng),則
上移動(dòng),則![]() D兩點(diǎn)間的最大距離為_______.
D兩點(diǎn)間的最大距離為_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個(gè)袋子中有4個(gè)紅球,2個(gè)白球,若從中任取2個(gè)球,則這2個(gè)球中有白球的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() 與
與![]() 的距離和它到直線
的距離和它到直線![]() 的距離的比是常數(shù)
的距離的比是常數(shù)![]() .
.
![]() 求點(diǎn)M的軌跡C的方程;
求點(diǎn)M的軌跡C的方程;
![]() 設(shè)N是圓E:
設(shè)N是圓E:![]() 上位于第四象限的一點(diǎn),過N作圓E的切線
上位于第四象限的一點(diǎn),過N作圓E的切線![]() ,與曲線C交于A,B兩點(diǎn)
,與曲線C交于A,B兩點(diǎn)![]() 求證:
求證:![]() 的周長(zhǎng)為10.
的周長(zhǎng)為10.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點(diǎn)
的焦點(diǎn)![]() ,
,![]() 上一點(diǎn)坐標(biāo)為
上一點(diǎn)坐標(biāo)為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)過![]() 作直線
作直線![]() ,交拋物線
,交拋物線![]() 于
于![]() ,
,![]() 兩點(diǎn),若直線
兩點(diǎn),若直線![]() 中點(diǎn)的縱坐標(biāo)為
中點(diǎn)的縱坐標(biāo)為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)生產(chǎn)甲、乙兩種產(chǎn)品均需要![]() ,
,![]() 兩種原料,已知生產(chǎn)1噸每種產(chǎn)品所需原料及每天原料的可用限額如表所示.如果生產(chǎn)1噸甲、乙產(chǎn)品可獲得利潤(rùn)分別為3萬(wàn)元、4萬(wàn)元,則該企業(yè)每天可獲得最大利潤(rùn)為( )
兩種原料,已知生產(chǎn)1噸每種產(chǎn)品所需原料及每天原料的可用限額如表所示.如果生產(chǎn)1噸甲、乙產(chǎn)品可獲得利潤(rùn)分別為3萬(wàn)元、4萬(wàn)元,則該企業(yè)每天可獲得最大利潤(rùn)為( )
甲 | 乙 | 原料限額 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10萬(wàn)元B. 12萬(wàn)元C. 13萬(wàn)元D. 14萬(wàn)元
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com