
���}Ŀ�����}�ģ����}�ģ���֪�E�A![]() ��������c(di��n)�քe��
��������c(di��n)�քe��![]() ��
��![]() ���ҽ��c(di��n)
���ҽ��c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ���c(di��n)
���c(di��n)![]() ����(bi��o)��
����(bi��o)��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �S���^(gu��)�c(di��n)
�S���^(gu��)�c(di��n)![]() ��ֱ��(xi��n)�c�E�A
��ֱ��(xi��n)�c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]() ��
��![]() �ڵ�һ�������c(di��n)
�ڵ�һ�������c(di��n)![]() ���c(di��n)
���c(di��n)![]() ���Ϸ�����ֱ��(xi��n)
���Ϸ�����ֱ��(xi��n)![]() �c
�c![]() �����c(di��n)
�����c(di��n)![]() ���B��
���B��![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() ����(w��n)��
����(w��n)��![]() ��б�ʳ˷e�Ƿ�鶨ֵ���������ԓ��ֵ�������ǣ��f(shu��)������.
��б�ʳ˷e�Ƿ�鶨ֵ���������ԓ��ֵ�������ǣ��f(shu��)������.
���𰸡���1��![]() ��2��
��2��![]() .
.
����������������1�����}���֪![]() ���t
���t![]() ��������ÙE�A����.
��������ÙE�A����.
��2�����}���O(sh��)![]() ��
��![]() ��
��![]() ���O(sh��)ֱ��(xi��n)
���O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ������E�A���̣���(xi��)���f�_(d��)�����P(gu��n)ϵʽ���ٸ���(j��)
������E�A���̣���(xi��)���f�_(d��)�����P(gu��n)ϵʽ���ٸ���(j��)![]() ���c(di��n)����(xi��n)���õ�
���c(di��n)����(xi��n)���õ�![]() ��Ȼ��Ӌ(j��)��
��Ȼ��Ӌ(j��)��![]() ��ֵ�鶨ֵ
��ֵ�鶨ֵ![]() .
.
Ԕ�⣺��1���O(sh��)�E�A���̞�![]() �����}���֪��
�����}���֪��![]() ������
������![]() ��
��
���ԙE�A�ķ��̞�![]()
��2���Ƕ�ֵ����ֵ��![]() .
.
�O(sh��)![]() ��
��![]() ����?y��n)�ֱ��(xi��n)
����?y��n)�ֱ��(xi��n)![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ���O(sh��)ֱ��(xi��n)
���O(sh��)ֱ��(xi��n)![]() �ķ��̞飺
�ķ��̞飺![]() ��
��
(li��n)��![]()
����![]() ��
��![]() ��
��
��?y��n)��c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ϣ����Կ��O(sh��)
�ϣ����Կ��O(sh��)![]() ��
��
��![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ϣ����ԣ�
�ϣ����ԣ�![]()
����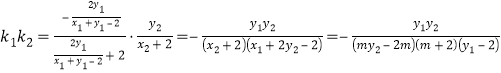
![]()



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����������߅![]() ��
��![]() ��
��![]() ��߅����������������
��߅����������������![]() ��
��![]() ��
��![]() ���t
���t![]() ��
��![]() ��
��![]() ����(xi��n)���c(di��n)��ԓ�c(di��n)�Q(ch��ng)��
����(xi��n)���c(di��n)��ԓ�c(di��n)�Q(ch��ng)��![]() �����Ƚ����ģ���(d��ng)
�����Ƚ����ģ���(d��ng)![]() ��ÿ��(g��)��(n��i)�Ƕ�С��120�r(sh��)�����Ƚ������c(di��n)P�M(m��n)���������|(zh��)��
��ÿ��(g��)��(n��i)�Ƕ�С��120�r(sh��)�����Ƚ������c(di��n)P�M(m��n)���������|(zh��)��
��1��![]() ����2�����Ƚ������ǵ�ԓ����������(g��)��c(di��n)���x֮����С���c(di��n)��Ҳ���M(f��i)�R�c(di��n)�������������|(zh��)��
����2�����Ƚ������ǵ�ԓ����������(g��)��c(di��n)���x֮����С���c(di��n)��Ҳ���M(f��i)�R�c(di��n)�������������|(zh��)��![]() ����Сֵ��_________
����Сֵ��_________
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���^(gu��)���タ(xi��n)![]() ���c(di��n)��ֱ��(xi��n)
���c(di��n)��ֱ��(xi��n)![]() �c���タ(xi��n)����
�c���タ(xi��n)����![]() ��
��![]() ���c(di��n)���c�A
���c(di��n)���c�A![]() ����
����![]() ��
��![]() ���c(di��n)���������lֱ��(xi��n)�M(m��n)��
���c(di��n)���������lֱ��(xi��n)�M(m��n)��![]() ���t
���t![]() ��ȡֵ�����飨 ��
��ȡֵ�����飨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x���Ƕ��x��R�ϵ�ż����(sh��)���Ү�(d��ng)x��0�r(sh��)��f��x����x2��2x��
��1����f��0����f��f��1������ֵ��
��2����(sh��)f��x���Ľ���ʽ��
��3�����P(gu��n)��x�ķ���f��x����m��0���Ă�(g��)��ͬ�Č�(sh��)��(sh��)�⣬��(sh��)��(sh��)m��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����![]() ����sin
����sin![]() ��cos
��cos![]() ��
��![]() .
.
(1)��cos ����ֵ��
(2)��sin(������)����![]() ������
������![]() ����cos ����ֵ��
����cos ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() �����c(di��n)���c(di��n)
�����c(di��n)���c(di��n)![]() �ھ�(xi��n)��
�ھ�(xi��n)��![]() �ϣ�
�ϣ�![]() ��
��![]() .
.
�������C��![]() ƽ��
ƽ��![]() ��
��
������![]() �����C��
�����C��![]() ƽ��
ƽ��![]() ��
��
������![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��3����![]() �cƽ��
�cƽ��![]() ���ɽǞ�
���ɽǞ�![]() ����
����![]() ���L(zh��ng)��
���L(zh��ng)��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D������һ��(g��)�L(zh��ng)���w�Π�ij��ڲ���������������߅�L(zh��ng)��20cm�������Σ��ߞ�30cm����(n��i)��20cm�����Һ���F(xi��n)���������Aбһ���Ƕ�![]() ���D�������҃Aб�r(sh��)�����һ�l��ʼ�K�������ϣ��D���������������Ŀv���棩��
���D�������҃Aб�r(sh��)�����һ�l��ʼ�K�������ϣ��D���������������Ŀv���棩��
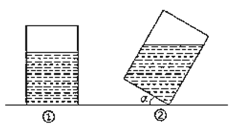
��1��Ҫʹ�Aб��������(n��i)����Һ����(hu��)�������![]() �����ֵ�Ƕ��٣�
�����ֵ�Ƕ��٣�
��2���F(xi��n)��Ҫ����������![]() ����Һ����(d��ng)
����Һ����(d��ng)![]() �r(sh��)���܌�(sh��)�F(xi��n)Ҫ��Ո(q��ng)�f(shu��)�����ɣ�
�r(sh��)���܌�(sh��)�F(xi��n)Ҫ��Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�����
�У�����![]() ��߅�L(zh��ng)��2�����Σ�
��߅�L(zh��ng)��2�����Σ�![]() ����(c��)��
����(c��)��![]() ������������(c��)��
������������(c��)��![]() ����
����![]() ��
��![]() ��
��![]() �քe����
�քe����![]() ��
��![]() �����c(di��n).
�����c(di��n).

�������C��![]() ƽ��
ƽ��![]() ��
��
�������C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��������![]() ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n)![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() �������ڣ���
�������ڣ���![]() ��ֵ���������ڣ�Ո(q��ng)�f(shu��)������.
��ֵ���������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com