
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系xoy中,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() 為參數(shù),
為參數(shù), ![]() 以原點O為極點,以
以原點O為極點,以![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為![]()
(1)寫出直線![]() 的極坐標(biāo)方程和曲線C的直角坐標(biāo)方程;
的極坐標(biāo)方程和曲線C的直角坐標(biāo)方程;
(2)若直線![]() 與曲線C相交于A,B 兩點,求
與曲線C相交于A,B 兩點,求![]() 的值.
的值.
【答案】(1)直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() 和
和![]() 曲線的直角坐標(biāo)方程為
曲線的直角坐標(biāo)方程為![]() (2)
(2) ![]()
【解析】試題分析:(1)將直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() 化為直角坐標(biāo)方程,利用
化為直角坐標(biāo)方程,利用![]() ,可得直線
,可得直線![]() 的極坐標(biāo)方程,再利用簡單的三角方程及極坐標(biāo)的幾何意義化簡可得直線
的極坐標(biāo)方程,再利用簡單的三角方程及極坐標(biāo)的幾何意義化簡可得直線![]() 的極坐標(biāo)方程,由
的極坐標(biāo)方程,由![]() 得
得![]() 利用
利用![]() 化簡可得曲線C的直角坐標(biāo)方程;(2)
化簡可得曲線C的直角坐標(biāo)方程;(2) ![]() 由
由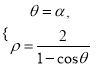 得,
得, ![]() 即
即![]() =
=![]() 同理可得
同理可得![]() =
=![]() ,從而可得
,從而可得![]() 的值.
的值.
試題解析:(1)由參數(shù)方程![]() 得當(dāng)
得當(dāng)![]() 時,直線
時,直線![]() 為
為![]() 其極坐標(biāo)方程為
其極坐標(biāo)方程為![]() 和
和![]()
當(dāng)![]() 時,消去參數(shù)
時,消去參數(shù)![]() 得
得![]() .因為
.因為![]() ,所以直線
,所以直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() 和
和![]()
綜合以上, 直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() 和
和![]()
由![]() 得
得![]() 因為
因為![]() 所以
所以![]() 化簡得曲線的直角坐標(biāo)方程為
化簡得曲線的直角坐標(biāo)方程為![]()
(2)設(shè)![]() 由
由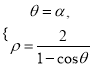 得,
得, ![]() 即|OA|=
即|OA|=![]() 同理
同理
由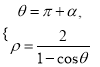 得,
得, ![]() 即|OB|=
即|OB|=![]() 所以
所以![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() +
+![]() =1(a>b>0)上的點P到左,右兩焦點F1,F2的距離之和為2
=1(a>b>0)上的點P到左,右兩焦點F1,F2的距離之和為2![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)過右焦點F2的直線l交橢圓于A,B兩點,若y軸上一點M(0,![]() )滿足|MA|=|MB|,求直線l的斜率k的值.
)滿足|MA|=|MB|,求直線l的斜率k的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某儀器經(jīng)過檢驗合格才能出廠,初檢合格率為![]() :若初檢不合格,則需要進(jìn)行調(diào)試,經(jīng)調(diào)試后再次對其進(jìn)行檢驗;若仍不合格,作為廢品處理,再檢合格率為
:若初檢不合格,則需要進(jìn)行調(diào)試,經(jīng)調(diào)試后再次對其進(jìn)行檢驗;若仍不合格,作為廢品處理,再檢合格率為![]() .每臺儀器各項費用如表:
.每臺儀器各項費用如表:
項目 | 生產(chǎn)成本 | 檢驗費/次 | 調(diào)試費 | 出廠價 |
金額(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每臺儀器能出廠的概率;
(Ⅱ)求生產(chǎn)一臺儀器所獲得的利潤為1600元的概率(注:利潤![]() 出廠價
出廠價![]() 生產(chǎn)成本
生產(chǎn)成本![]() 檢驗費
檢驗費![]() 調(diào)試費);
調(diào)試費);
(Ⅲ)假設(shè)每臺儀器是否合格相互獨立,記![]() 為生產(chǎn)兩臺儀器所獲得的利潤,求
為生產(chǎn)兩臺儀器所獲得的利潤,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】PM2.5是指大氣中直徑小于或等于2.5微米的顆粒物,也稱為可入肺顆粒物.我國PM2.5標(biāo)準(zhǔn)采用世衛(wèi)組織設(shè)定的最寬限值,即PM2.5日均在35微克/立方米以下空氣質(zhì)量為一級,在35微克/立方米![]() 75微克/立方米之間空氣質(zhì)量為二級,在75微克/立方米以上空氣質(zhì)量為超標(biāo).北方某市環(huán)保局從2015年全年每天的PM2.5監(jiān)測數(shù)據(jù)中隨機抽取15天的數(shù)據(jù)作為樣本,監(jiān)測值如下圖所示(十位為莖,個位為葉).
75微克/立方米之間空氣質(zhì)量為二級,在75微克/立方米以上空氣質(zhì)量為超標(biāo).北方某市環(huán)保局從2015年全年每天的PM2.5監(jiān)測數(shù)據(jù)中隨機抽取15天的數(shù)據(jù)作為樣本,監(jiān)測值如下圖所示(十位為莖,個位為葉).

(1)15天的數(shù)據(jù)中任取3天的數(shù)據(jù),記![]() 表示其中空氣質(zhì)量達(dá)到一級的天數(shù),求
表示其中空氣質(zhì)量達(dá)到一級的天數(shù),求![]() 的分布列;
的分布列;
(2)以這15天的PM2.5日均值來估計一年的空氣質(zhì)量情況,則一年(按360天計算)中大約有多少天的空氣質(zhì)量達(dá)到一級.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個生產(chǎn)公司投資A生產(chǎn)線500萬元,每萬元可創(chuàng)造利潤![]() 萬元,該公司通過引進(jìn)先進(jìn)技術(shù),在生產(chǎn)線A投資減少了x萬元,且每萬元的利潤提高了
萬元,該公司通過引進(jìn)先進(jìn)技術(shù),在生產(chǎn)線A投資減少了x萬元,且每萬元的利潤提高了![]() ;若將少用的x萬元全部投入B生產(chǎn)線,每萬元創(chuàng)造的利潤為
;若將少用的x萬元全部投入B生產(chǎn)線,每萬元創(chuàng)造的利潤為![]() 萬元,其中
萬元,其中![]() .
.
![]() 若技術(shù)改進(jìn)后A生產(chǎn)線的利潤不低于原來A生產(chǎn)線的利潤,求x的取值范圍;
若技術(shù)改進(jìn)后A生產(chǎn)線的利潤不低于原來A生產(chǎn)線的利潤,求x的取值范圍;
![]() 若生產(chǎn)線B的利潤始終不高于技術(shù)改進(jìn)后生產(chǎn)線A的利潤,求a的最大值.
若生產(chǎn)線B的利潤始終不高于技術(shù)改進(jìn)后生產(chǎn)線A的利潤,求a的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某大學(xué)志愿者協(xié)會有6名男同學(xué),4名女同學(xué),在這10名同學(xué)中,3名同學(xué)來自數(shù)學(xué)學(xué)院,其余7名同學(xué)來自物理﹑化學(xué)等其他互不相同的七個學(xué)院,現(xiàn)從這10名同學(xué)中隨機選取3名同學(xué),到希望小學(xué)進(jìn)行支教活動(每位同學(xué)被選到的可能性相同).
(1)求選出的3名同學(xué)是來自互不相同學(xué)院的概率;
(2)設(shè)![]() 為選出的3名同學(xué)中女同學(xué)的人數(shù),求隨機變量
為選出的3名同學(xué)中女同學(xué)的人數(shù),求隨機變量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線![]() 的焦點是橢圓
的焦點是橢圓![]() 的頂點,
的頂點, ![]() 為橢圓
為橢圓![]() 的左焦點且橢圓
的左焦點且橢圓![]() 經(jīng)過點
經(jīng)過點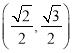 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的右頂點
的右頂點![]() 作斜率為
作斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于另一點
于另一點![]() ,連結(jié)
,連結(jié)![]() 并延長
并延長![]() 交橢圓
交橢圓![]() 于點
于點![]() ,當(dāng)
,當(dāng)![]() 的面積取得最大值時,求
的面積取得最大值時,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,上頂點為
,上頂點為![]() 為坐標(biāo)原點,橢圓的離心率
為坐標(biāo)原點,橢圓的離心率![]() 且
且![]() 的面積為
的面積為![]() .
.
(1)求橢圓的方程;
(2)設(shè)線段![]() 的中點為
的中點為![]() ,經(jīng)過
,經(jīng)過![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,
兩點, ![]() ,若點
,若點![]() 關(guān)于
關(guān)于![]() 軸的對稱點在直線
軸的對稱點在直線![]() 上,求直線
上,求直線![]() 方程.
方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com