
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 的單調區間.
的單調區間.
(2)設直線![]() 是曲線
是曲線![]() 的切線,若
的切線,若![]() 的斜率存在最小值-2,求
的斜率存在最小值-2,求![]() 的值,并求取得最小斜率時切線
的值,并求取得最小斜率時切線![]() 的方程.
的方程.
(3)已知![]() 分別在
分別在![]() ,
,![]() 處取得極值,求證:
處取得極值,求證:![]() .
.
【答案】(1)單調遞增區間為![]() ,
,![]() ;單調遞減區間為
;單調遞減區間為![]() ;(2)
;(2)![]() ,
,![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)由![]() 的正負可確定
的正負可確定![]() 的單調區間;
的單調區間;
(2)利用基本不等式可求得![]() 時,
時,![]() 取得最小值
取得最小值![]() ,由導數的幾何意義可知
,由導數的幾何意義可知![]() ,從而求得
,從而求得![]() ,求得切點坐標
,求得切點坐標![]() 后,可得到切線方程;
后,可得到切線方程;
(3)由極值點的定義可知![]() 是
是![]() 的兩個不等正根,由判別式大于零得到
的兩個不等正根,由判別式大于零得到![]() 的取值范圍,同時得到韋達定理的形式;化簡
的取值范圍,同時得到韋達定理的形式;化簡![]() 為
為![]() ,結合
,結合![]() 的范圍可證得結論.
的范圍可證得結論.
(1)由題意得:![]() 的定義域為
的定義域為![]() ,
,
當![]() 時,
時,![]() ,
,
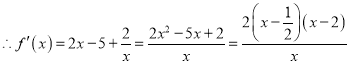 ,
,
![]() 當
當![]() 和
和![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ;單調遞減區間為
;單調遞減區間為![]() .
.
(2)![]() ,所以
,所以![]() (當且僅當
(當且僅當![]() ,即
,即![]() 時取等號),
時取等號),
![]() 切線
切線![]() 的斜率存在最小值
的斜率存在最小值![]() ,
,![]() ,解得:
,解得:![]() ,
,
![]() ,即切點為
,即切點為![]() ,
,
從而切線方程![]() ,即:
,即:![]() .
.
(3)![]() ,
,
![]() 分別在
分別在![]() ,
,![]() 處取得極值,
處取得極值,
![]() ,
,![]() 是方程
是方程![]() ,即
,即![]() 的兩個不等正根.
的兩個不等正根.
則![]() ,解得:
,解得:![]() ,且
,且![]() ,
,![]() .
.
![]()
![]()
![]() ,
,
![]() ,
,![]() ,
,
即不等式![]() 成立.
成立.


科目:高中數學 來源: 題型:
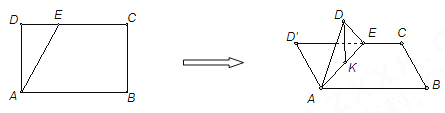
【題目】如圖,在長方形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為線段
為線段![]() 上一動點,現將
上一動點,現將![]() 沿
沿![]() 折起,使點
折起,使點![]() 在面
在面![]() 內的射影
內的射影![]() 在直線
在直線![]() 上,當點
上,當點![]() 從
從![]() 運動到
運動到![]() ,則點
,則點![]() 所形成軌跡的長度為( )
所形成軌跡的長度為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(x>0).
,(x>0).
(1)當0<a<b,且f(a)=f(b)時,求證:ab>1;
(2)是否存在實數a,b(a<b),使得函數y=f(x)的定義域、值域都是[a,b],若存在,則求出a,b的值,若不存在,請說明理由.
(3)若存在實數a,b(a<b),使得函數y=f(x)的定義域為[a,b]時,值域為[ma,mb](m≠0),求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,已知每售出一箱酸奶的利潤為50元,當天未售出的酸奶降價處理,以每箱虧損10元的價格全部處理完.若供不應求,可從其它商店調撥,每銷售1箱可獲利30元.假設該超市每天的進貨量為14箱,超市的日利潤為y元.為確定以后的訂購計劃,統計了最近50天銷售該酸奶的市場日需求量,其頻率分布表如圖所示.
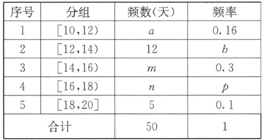
(1)求![]() 的值;
的值;
(2)求y關于日需求量![]() 的函數表達式;
的函數表達式;
(3)以50天記錄的酸奶需求量的頻率作為酸奶需求量發生的概率,估計日利潤在區間[580,760]內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知點
中,已知點![]() ,圓
,圓![]() :
:![]() 與
與![]() 軸的正半軸的交點是
軸的正半軸的交點是![]() ,過點
,過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() .
.

(1)若直線![]() 與
與![]() 軸交于
軸交于![]() ,且
,且![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設直線![]() ,
,![]() 的斜率分別是
的斜率分別是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)設![]() 的中點為
的中點為![]() ,點
,點![]() ,若
,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體![]() 中,E是棱
中,E是棱![]() 的中點,F是側面
的中點,F是側面![]() 內的動點,且
內的動點,且![]() 與平面
與平面![]() 的垂線垂直,如圖所示,下列說法不正確的是( )
的垂線垂直,如圖所示,下列說法不正確的是( )
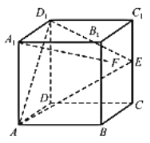
A.點F的軌跡是一條線段B.![]() 與BE是異面直線
與BE是異面直線
C.![]() 與
與![]() 不可能平行D.三棱錐
不可能平行D.三棱錐![]() 的體積為定值
的體積為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠家具車間造A、B型兩類桌子,每張桌子需木工和漆工兩道工序完成.已知木工做一張A、B型桌子分別需要1小時和2小時,漆工油漆一張A、B型桌子分別需要3小時和1小時;又知木工、漆工每天工作分別不得超過8小時和9小時,而工廠造一張A、B型桌子分別獲利潤2千元和3千元,試問工廠每天應生產A、B型桌子各多少張,才能獲得利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com