
【題目】已知{an}是各項均為正數的等比數列,且a1+a2=6,a1a2=a3.
(1)求數列{an}的通項公式;
(2){bn}為各項非零的等差數列,其前n項和為Sn.已知S2n+1=bnbn+1,求數列{![]() }的前n項和Tn.
}的前n項和Tn.
科目:高中數學 來源: 題型:
【題目】探究與發現:為什么二次函數![]() 的圖象是拋物線?我們知道,平面內與一個定點F和一條定直線l距離相等的點的軌跡是拋物線,這是拋物線的定義,也是其本質特征
的圖象是拋物線?我們知道,平面內與一個定點F和一條定直線l距離相等的點的軌跡是拋物線,這是拋物線的定義,也是其本質特征![]() 因此,只要說明二次函數的圖象符合拋物線的本質特征,就解決了為什么二次函數
因此,只要說明二次函數的圖象符合拋物線的本質特征,就解決了為什么二次函數![]() 的圖象是拋物線的問題
的圖象是拋物線的問題![]() 進一步講,由拋物線與其方程之間的關系可知,如果能用適當的方式將
進一步講,由拋物線與其方程之間的關系可知,如果能用適當的方式將![]() 轉化為拋物線標準方程的形式,那么就可以判定二次函數
轉化為拋物線標準方程的形式,那么就可以判定二次函數![]() 的圖象是拋物線了.下面我們就按照這個思路來展開.對二次函數式
的圖象是拋物線了.下面我們就按照這個思路來展開.對二次函數式![]() 的右邊配方,得
的右邊配方,得![]() .由函數圖象平移
.由函數圖象平移![]() 一般地,設
一般地,設![]() 是坐標平面內的一個圖形,將
是坐標平面內的一個圖形,將![]() 上所有點按照同一方向,移動同樣的長度,得到圖形
上所有點按照同一方向,移動同樣的長度,得到圖形![]() ,這一過程叫作圖形的平移
,這一過程叫作圖形的平移![]() 的知識可以知道,沿向量
的知識可以知道,沿向量![]() 平移函數
平移函數![]() 的圖象
的圖象![]() 如圖,函數圖象的形狀、大小不發生任何變化,平移后圖象對應的函數解析式為
如圖,函數圖象的形狀、大小不發生任何變化,平移后圖象對應的函數解析式為![]() ,我們把它改寫為
,我們把它改寫為![]() 的形式
的形式![]() 方程
方程![]() ,這是頂點為坐標原點,焦點為
,這是頂點為坐標原點,焦點為![]() 的拋物線.這樣就說明了二次函數
的拋物線.這樣就說明了二次函數![]() 的圖象是一條拋物線.
的圖象是一條拋物線.
請根據以上閱讀材料,回答下列問題:
![]() 由函數
由函數![]() 的圖象沿向量
的圖象沿向量![]() 平移,得到的圖象對應的函數解析式為
平移,得到的圖象對應的函數解析式為![]() ,求
,求![]() 的坐標;
的坐標;
![]() 過拋物線
過拋物線![]() 的焦點F的一條直線交拋物線于P、Q兩點若線段PF與QF的長分別是p、q,試探究
的焦點F的一條直線交拋物線于P、Q兩點若線段PF與QF的長分別是p、q,試探究![]() 是否為定值?并說明理由.
是否為定值?并說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
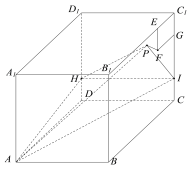
【題目】如圖所示,正方體ABCD﹣A1B1C1D1棱長為4,點![]() 在棱
在棱![]() 上,點
上,點![]() 在棱
在棱![]() 上,且
上,且![]() .在側面
.在側面![]() 內以
內以![]() 為一個頂點作邊長為1的正方形
為一個頂點作邊長為1的正方形![]() ,側面
,側面![]() 內動點
內動點![]() 滿足到平面
滿足到平面![]() 距離等于線段
距離等于線段![]() 長的
長的![]() 倍,則當點
倍,則當點![]() 運動時,三棱錐
運動時,三棱錐![]() 的體積的最小值是( )
的體積的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為保障公平性,高考時每個考點都要安裝手機屏蔽儀,要求在考點周圍1千米處不能收到手機信號,如圖,檢查員抽查某市一考點![]() ,以考點
,以考點![]() 正西
正西![]() 千米的
千米的![]() 處開始為檢查起點,沿著一條北偏東
處開始為檢查起點,沿著一條北偏東![]() 方向的公路
方向的公路![]() ,以每小時12千米的速度行駛,并用手機接通電話,問從起點開始計時,最長經過多少分鐘檢查員開始收不到信號(
,以每小時12千米的速度行駛,并用手機接通電話,問從起點開始計時,最長經過多少分鐘檢查員開始收不到信號(![]() 點開始),并至少持續多長時間(
點開始),并至少持續多長時間(![]() 之間)該考點才算檢查合格?
之間)該考點才算檢查合格?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖在直角坐標系中,![]() 的圓心角為
的圓心角為![]() ,
,![]() 所在圓的半徑為1,角θ的終邊與
所在圓的半徑為1,角θ的終邊與![]() 交于點C.
交于點C.

(1)當C為![]() 的中點時,D為線段OA上任一點,求
的中點時,D為線段OA上任一點,求![]() 的最小值;
的最小值;
(2)當C在![]() 上運動時,D,E分別為線段OA,OB的中點,求
上運動時,D,E分別為線段OA,OB的中點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在區間![]() 上的兩個函數
上的兩個函數![]() 和
和![]() ,如果對任意的
,如果對任意的![]() ,均有不等式
,均有不等式![]() 成立,則稱函數
成立,則稱函數![]() 與
與![]() 在
在![]() 上是“友好”的,否則稱為“不友好”的.
上是“友好”的,否則稱為“不友好”的.
(1)若![]() ,
,![]() ,則
,則![]() 與
與![]() 在區間
在區間![]() 上是否“友好”;
上是否“友好”;
(2)現在有兩個函數![]() 與
與![]() ,給定區間
,給定區間![]() .
.
①若![]() 與
與![]() 在區間
在區間![]() 上都有意義,求
上都有意義,求![]() 的取值范圍;
的取值范圍;
②討論函數![]() 與
與![]() 與在區間
與在區間![]() 上是否“友好”.
上是否“友好”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com