
【題目】已知![]() .
.
(1)若![]() 在
在![]() 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)證明:當(dāng)![]() 時(shí),
時(shí),![]() .
.
【答案】(1) ![]() (2)證明見解析
(2)證明見解析
【解析】
(1)求導(dǎo)![]() ,
,![]() ,討論
,討論![]() 與1 的大小確定
與1 的大小確定![]() 的正負(fù),進(jìn)而確定
的正負(fù),進(jìn)而確定![]() 的最值即可證明
的最值即可證明
(2)由(1)取![]() ,得
,得![]() ,要證
,要證![]() ,只需證
,只需證![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,證明
,證明![]() 即可證明
即可證明
(1)法一:由題意![]() ,
,![]()
① 若![]() ,即
,即![]() 時(shí),
時(shí),![]() ,則
,則![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
則![]() ,則
,則![]() 在
在![]() 單調(diào)遞增,故
單調(diào)遞增,故![]() ,滿足題意;
,滿足題意;
② 若![]() ,即
,即![]() 時(shí),存在
時(shí),存在![]() ,使得
,使得![]() ,且當(dāng)
,且當(dāng)![]() 時(shí),
時(shí),![]() ,則
,則![]() 在
在![]() 上單調(diào)遞減,則
上單調(diào)遞減,則![]() ,則
,則![]() 在
在![]() 單調(diào)遞減,此時(shí)
單調(diào)遞減,此時(shí)![]() ,舍去;
,舍去;
③ 若![]() ,即
,即![]() 時(shí),
時(shí),![]() ,則
,則![]() 在
在![]() 上單調(diào)遞減,則
上單調(diào)遞減,則![]() ,則
,則![]() 在
在![]() 單調(diào)遞減,
單調(diào)遞減, ![]() ,舍去;
,舍去;
故![]() .
.
法二:由題知![]() ,且
,且![]() ,
,![]() ,
,![]()
要使得![]() 在
在![]() 上恒成立,則必須滿足
上恒成立,則必須滿足![]() ,即
,即![]() ,
,![]() .
.
① 若![]() 時(shí),
時(shí),![]() ,則
,則![]() 在
在![]() 單調(diào)遞增,則
單調(diào)遞增,則![]() ,
,
則![]() 在
在![]() 單調(diào)遞增,故
單調(diào)遞增,故![]() ,滿足題意;
,滿足題意;
② 若![]() 時(shí),存在
時(shí),存在![]() 時(shí),
時(shí),![]() ,則
,則![]() 在
在![]() 上單調(diào)遞減,則
上單調(diào)遞減,則![]() ,則
,則![]() 在
在![]() 單調(diào)遞減,此時(shí)
單調(diào)遞減,此時(shí)![]() ,舍去;
,舍去;
故![]() .
.
(2)證明:由(1)知,當(dāng)![]() 時(shí),
時(shí),![]() .取
.取![]() ,
,
則![]()
由(1)![]() ,則
,則![]() ,故
,故![]() ,
,
要證![]() ,只需證
,只需證![]() .
.
令![]() ,則
,則![]() ,
,![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,則
,則![]() 在
在![]() 上單調(diào)遞增,有
上單調(diào)遞增,有![]() ,
,
故![]() 在
在![]() 單調(diào)遞增,故
單調(diào)遞增,故![]() ,
,
故![]() ,即有
,即有![]() ,得證
,得證



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,函數(shù)
,函數(shù)![]() 為
為![]() 的導(dǎo)函數(shù).
的導(dǎo)函數(shù).
(1)若![]() ,都有
,都有![]() 成立(其中
成立(其中![]() ),求
),求![]() 的值;
的值;
(2)證明:當(dāng)![]() 時(shí),
時(shí),![]() ;
;
(3)設(shè)當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,以
中,以![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 的參數(shù)方程為
的參數(shù)方程為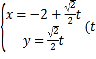 為參數(shù)
為參數(shù)![]() ,直線
,直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點(diǎn).
兩點(diǎn).
(1)若點(diǎn)![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,求
,求![]() 的值;
的值;
(2)求曲線![]() 的內(nèi)接矩形周長(zhǎng)的最大值.
的內(nèi)接矩形周長(zhǎng)的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題中,說法正確的個(gè)數(shù)是( )
(1)若p![]() q為真命題,則p,q均為真命題
q為真命題,則p,q均為真命題
(2)命題“x0∈R,![]() 0”的否定是“x∈R,2x
0”的否定是“x∈R,2x![]() 0”
0”
(3)“![]() ”是“x∈[1,2],x2﹣
”是“x∈[1,2],x2﹣![]() 恒成立”的充分條件
恒成立”的充分條件
(4)在△ABC中,“![]() ”是“sinA>sinB”的必要不充分條件
”是“sinA>sinB”的必要不充分條件
(5)命題“若x2=1,則x=1”的否命題為:“若x2=1,則x≠1”
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】命題p:![]() x∈R,ax2﹣2ax+1>0,命題q:指數(shù)函數(shù)f(x)=ax(a>0且a≠1)為減函數(shù),則P是q的( )
x∈R,ax2﹣2ax+1>0,命題q:指數(shù)函數(shù)f(x)=ax(a>0且a≠1)為減函數(shù),則P是q的( )
A.充分不必要條件B.必要不充分條件
C.充分必要條件D.既不充分也不必要條件
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知直線
中,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為![]()
![]() .以坐標(biāo)原點(diǎn)
.以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的非負(fù)半軸為極軸,取相同的長(zhǎng)度單位建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸,取相同的長(zhǎng)度單位建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若曲線![]() 上的點(diǎn)到直線l的最大距離為
上的點(diǎn)到直線l的最大距離為![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)橢圓![]() :
:![]() 的左焦點(diǎn)為
的左焦點(diǎn)為![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
(1)若點(diǎn)![]() 也是頂點(diǎn)為原點(diǎn)的拋物線
也是頂點(diǎn)為原點(diǎn)的拋物線![]() 的焦點(diǎn),求拋物線
的焦點(diǎn),求拋物線![]() 的方程;
的方程;
(2)當(dāng)![]() 與
與![]() 軸垂直時(shí),求直線
軸垂直時(shí),求直線![]() 的方程;
的方程;
(3)設(shè)![]() 為坐標(biāo)原點(diǎn),證明:
為坐標(biāo)原點(diǎn),證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)![]() ,當(dāng)
,當(dāng)![]() 時(shí),對(duì)任意
時(shí),對(duì)任意![]() ,存在
,存在![]() ,使
,使![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com