
【題目】已知函數f(x)= 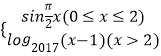 ,若a,b,c互不相等,且f(a)=f(b)=f(c),則a+b+c的取值范圍是( )
,若a,b,c互不相等,且f(a)=f(b)=f(c),則a+b+c的取值范圍是( )
A.(4,2018)
B.(4,2020)
C.(3,2020)
D.(2,2020)
科目:高中數學 來源: 題型:
【題目】三國時代吳國數學家趙爽所注《周髀算經》中給出了勾股定理的絕妙證明,下面是趙爽的弦圖及注文,弦圖是一個以勾股形之弦為邊的正方形,其面積稱為弦實,圖中包含四個全等的勾股形及一個小正方形,分別涂成紅(朱)色及黃色,其面積稱為朱實,黃實,利用2×勾×股+(股﹣勾)2=4×朱實+黃實=弦實,化簡,得勾2+股2=弦2 , 設勾股中勾股比為1: ![]() ,若向弦圖內隨機拋擲1000顆圖釘(大小忽略不計),則落在黃色圖形內的圖釘數大約為( )
,若向弦圖內隨機拋擲1000顆圖釘(大小忽略不計),則落在黃色圖形內的圖釘數大約為( ) 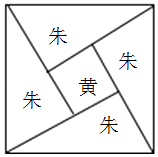
A.866
B.500
C.300
D.134
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓錐曲線 ![]() (
( ![]() 是參數)和定點
是參數)和定點 ![]() ,
, ![]() 、
、 ![]() 是圓錐曲線的左、右焦點.
是圓錐曲線的左、右焦點.
(1)求經過點 ![]() 且垂直于直線
且垂直于直線 ![]() 的直線
的直線 ![]() 的參數方程;
的參數方程;
(2)以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,求直線
軸的正半軸為極軸建立極坐標系,求直線 ![]() 的極坐標方程.
的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x,y∈R,且  ,則存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)構成的區域面積為( )
,則存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)構成的區域面積為( )
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]() ﹣
﹣ ![]()
C.![]()
D.![]() +
+ ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系下,知圓O:ρ=cosθ+sinθ和直線 ![]() .
.
(1)求圓O與直線l的直角坐標方程;
(2)當θ∈(0,π)時,求圓O和直線l的公共點的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() :
: ![]() 的離心率為
的離心率為 ![]() ,且以兩焦點為直徑的圓的內接正方形面積為2.
,且以兩焦點為直徑的圓的內接正方形面積為2.
(1)求橢圓 ![]() 的標準方程;
的標準方程;
(2)若直線 ![]() :
: ![]() 與橢圓
與橢圓 ![]() 相交于
相交于 ![]() ,
, ![]() 兩點,在
兩點,在 ![]() 軸上是否存在點
軸上是否存在點 ![]() ,使直線
,使直線 ![]() 與
與 ![]() 的斜率之和
的斜率之和 ![]() 為定值?若存在,求出點
為定值?若存在,求出點 ![]() 坐標及該定值,若不存在,試說明理由.
坐標及該定值,若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
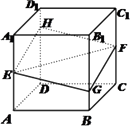
【題目】如圖,正方體 ![]() 的棱長為1,
的棱長為1, ![]() 分別是棱
分別是棱 ![]() 的中點,過
的中點,過 ![]() 的平面與棱
的平面與棱 ![]() 分別交于點
分別交于點 ![]() .設
.設 ![]() ,
, ![]() .
.
①四邊形 ![]() 一定是菱形;②
一定是菱形;② ![]() 平面
平面 ![]() ;③四邊形
;③四邊形 ![]() 的面積
的面積 ![]() 在區間
在區間 ![]() 上具有單調性;④四棱錐
上具有單調性;④四棱錐 ![]() 的體積為定值.
的體積為定值.
以上結論正確的個數是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com