【題目】已知 
為等差數(shù)列，公差 
（ 
），且
（ 
）
（1）求證：當(dāng) 
取不同自然數(shù)時，此方程有公共根；
（2）若方程不同的根依次為
， 
， 
， …，
， …，求證：數(shù)列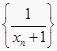 
為等差數(shù)列。
【答案】
（1）因?yàn)?是等差數(shù)列， ，
故方程 可變?yōu)?，
當(dāng) 取不同自然數(shù)時，方程有一個公共根 。
（2）方程的非公共根為 ，
是等差數(shù)列。
【解析】分析：（1）根據(jù)等差數(shù)列的性質(zhì)可得 
，故方程
可變?yōu)?
即可；（2）本題是考查等差關(guān)系的確定，考查了學(xué)生的推理運(yùn)算能力，屬于難題。
【考點(diǎn)精析】通過靈活運(yùn)用等差數(shù)列的性質(zhì)，掌握在等差數(shù)列{an}中，從第2項(xiàng)起，每一項(xiàng)是它相鄰二項(xiàng)的等差中項(xiàng)；相隔等距離的項(xiàng)組成的數(shù)列是等差數(shù)列即可以解答此題．
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓C： 
(a>b>0)的一個頂點(diǎn)為A(2,0)，離心率為
.直線y＝k(x－1)與橢圓C交于不同的兩點(diǎn)M，N.
(1)求橢圓C的方程；
(2)當(dāng)△AMN的面積為
時，求k的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某人上午7時乘船出發(fā)，以勻速
海里/小時
從
港前往相距50海里的
港，然后乘汽車以勻速
千米/小時(
)自
港前往相距
千米的
市，計(jì)劃當(dāng)天下午4到9時到達(dá)
市.設(shè)乘船和汽車的所要的時間分別為
、
小時，如果所需要的經(jīng)費(fèi)
(單位：元)
(1)試用含有
、
的代數(shù)式表示
；
(2)要使得所需經(jīng)費(fèi)
最少，求
和
的值，并求出此時的費(fèi)用.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】等差數(shù)列{an}的前n項(xiàng)和為Sn ， 若a7＞0，a8＜0，則下列結(jié)論正確的是( )
A.S7＜S8
B.S15＜S16
C.S13＞0
D.S15＞0
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知Sn表示數(shù)列{an}的前n項(xiàng)和，若對任意的n∈N*滿足an＋1＝an＋a2 ， 且a3＝2，則S2016＝( )
A.1006×2013
B.1006×2014
C.1008×2015
D.1007×2015
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如下圖所示將若干個點(diǎn)擺成三角形圖案，每條邊（包括兩個端點(diǎn)）有n(n>l，n∈N*)個點(diǎn)，相應(yīng)的圖案中總的點(diǎn)數(shù)記為 
，則 
… 
=（ ）． 
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)F（x）=|lgx|，若0＜a＜b，且f（a）=f（b），則a+2b的取值范圍是（ ）
A.
B.
C.（3，+∞）
D.[3，+∞）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
=lnx+ax2+(2a+1)x．
（1）討論
的單調(diào)性；
（2）當(dāng)a﹤0時，證明
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若y=|3sin（ωx+ 
）+2|的圖象向右平移 
個單位后與自身重合，且y=tanωx的一個對稱中心為（ 
，0），則ω的最小正值為 ．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com