Question

【題目】如圖，在四棱錐P－ABCD中，平面PAD⊥平面ABCD，AB＝AD，∠BAD＝60°，E，F分別是AP，AD的中點．

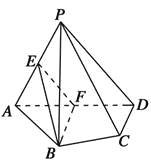
求證：（1）直線EF∥平面PCD；

（2）平面BEF⊥平面PAD．

Answer 1

【答案】（1）詳見解析（2）詳見解析

【解析】試題分析：（1）要證直線EF∥平面PCD，只需證明EF∥PD，EF不在平面PCD中，PD平面PCD即可；（2）連接BD，證明BF⊥AD．說明平面PAD∩平面ABCD=AD，推出BF⊥平面PAD；然后證明平面BEF⊥平面PAD

試題解析：（1）在△PAD中，因為E，F分別為AP，AD的中點，所以EF∥PD．

又因為EF不在平面PCD中，PD?平面PCD

所以直線EF∥平面PCD．

（2）連接BD．因為AB=AD，∠BAD=60°．

所以△ABD為正三角形．因為F是AD的中點，所以BF⊥AD．

因為平面PAD⊥平面ABCD，BF?平面ABCD，

平面PAD∩平面ABCD=AD，所以BF⊥平面PAD．

又因為BF平面EBF，所以平面BEF⊥平面PAD