
【題目】已知各項均為正數的無窮數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() (其中
(其中![]() 為常數),
為常數),![]()
![]() .數列
.數列![]() 滿足
滿足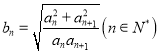 .
.
(1)證明數列![]() 是等差數列,并求出
是等差數列,并求出![]() 的通項公式;
的通項公式;
(2)若無窮等比數列![]() 滿足:對任意的
滿足:對任意的![]() ,數列
,數列![]() 中總存在兩個不同的項
中總存在兩個不同的項![]() ,
, ![]()
![]() 使得
使得![]() ,求
,求![]() 的公比
的公比![]() .
.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)仿寫式子,兩式相減得到![]() ,利用等差數列的定義和通項公式進行求解;(2)構造數列,利用遞減數列得到取值范圍,利用數列是特殊的函數,利用導數研究其單調性,利用
,利用等差數列的定義和通項公式進行求解;(2)構造數列,利用遞減數列得到取值范圍,利用數列是特殊的函數,利用導數研究其單調性,利用![]() 確定公比的取值.
確定公比的取值.
試題解析:(1)方法一:因為![]() ①,
①,
所以![]() ②,
②,
由②-①得, ![]()
![]() ,
,
即![]()
![]() ,又
,又![]() ,
,
則![]() ,即
,即![]() .
.
在![]() 中令
中令![]() 得,
得, ![]() ,即
,即![]() .
.
綜上,對任意![]() ,都有
,都有![]() ,
,
故數列![]() 是以
是以![]() 為公差的等差數列.
為公差的等差數列.
又![]() ,則
,則![]() .
.
方法二:因為![]() ,所以
,所以![]() ,又
,又![]() ,
,
則數列![]() 是以
是以![]() 為首項,
為首項, ![]() 為公差的等差數列,
為公差的等差數列,
因此![]() ,即
,即![]() .
.
當![]() 時,
時, ![]() ,又
,又![]() 也符合上式,
也符合上式,
故![]() .
.
故對任意![]() ,都有
,都有![]() ,即數列
,即數列![]() 是以
是以![]() 為公差的等差數列.
為公差的等差數列.
(2)令![]() ,則數列
,則數列![]() 是遞減數列,所以
是遞減數列,所以![]() .
.
考察函數![]() ,因為
,因為![]() ,所以
,所以![]() 在
在![]() 上遞增,因此
上遞增,因此![]() ,從而
,從而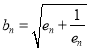
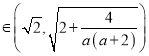 .
.
因為對任意![]() ,總存在數列
,總存在數列![]() 中的兩個不同項
中的兩個不同項![]() ,
, ![]() ,使得
,使得![]() ,所以對任意的
,所以對任意的![]() 都有
都有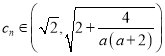 ,明顯
,明顯![]() .
.
若![]() ,當
,當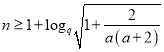 時,
時,
有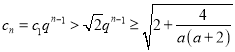 ,不符合題意,舍去;
,不符合題意,舍去;
若![]() ,當
,當![]() 時,
時,
有![]()
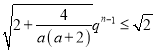 ,不符合題意,舍去;
,不符合題意,舍去;
故![]() .
.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數學 來源: 題型:
【題目】4月23日是“世界讀書日”,某中學在此期間開展了一系列的讀書教育活動.為了解高三學生課外閱讀情況,采用分層抽樣的方法從高三某班甲、乙、丙、丁四個小組中隨機抽取10名學生參加問卷調查.各組人數統計如下:

(1)從參加問卷調查的10名學生中隨機抽取兩名,求這兩名學生來自同一個小組的概率;
(2)在參加問卷調查的10名學生中,從來自甲、丙兩個小組的學生中隨機抽取兩名,用![]() 表示抽得甲組學生的人數,求
表示抽得甲組學生的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對任意實數![]() ,
,![]() ,
,![]() ,給出下列命題,其中真命題是( )
,給出下列命題,其中真命題是( )
A.“![]() ”是“
”是“![]() ”的充要條件B.“
”的充要條件B.“![]() ”是“
”是“![]() ”的充分條件
”的充分條件
C.“![]() ”是“
”是“![]() ”的必要條件D.“
”的必要條件D.“![]() 是無理數”是“
是無理數”是“![]() 是無理數”的充要條件
是無理數”的充要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)已知函數f(x)=![]()
(1)判斷函數在區間[1,+∞)上的單調性,并用定義證明你的結論.
(2)求該函數在區間[1,4]上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正四棱錐![]() 的側棱和底面邊長相等,在這個正四棱錐的
的側棱和底面邊長相等,在這個正四棱錐的![]() 條棱中任取兩條,按下列方式定義隨機變量
條棱中任取兩條,按下列方式定義隨機變量![]() 的值:
的值:
若這兩條棱所在的直線相交,則![]() 的值是這兩條棱所在直線的夾角大小(弧度制);
的值是這兩條棱所在直線的夾角大小(弧度制);
若這兩條棱所在的直線平行,則![]() ;
;
若這兩條棱所在的直線異面,則![]() 的值是這兩條棱所在直線所成角的大小(弧度制).
的值是這兩條棱所在直線所成角的大小(弧度制).
(1)求![]() 的值;
的值;
(2)求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,若直線
兩點,若直線![]() 與
與![]() 斜率之積為
斜率之積為![]() ,求證:直線
,求證:直線![]() 過定點,并求定點坐標.
過定點,并求定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 有極值,且函數
有極值,且函數![]() 的極值點是
的極值點是![]() 的極值點,其中
的極值點,其中![]() 是自然對數的底數.(極值點是指函數取得極值時對應的自變量的值)
是自然對數的底數.(極值點是指函數取得極值時對應的自變量的值)
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)當![]() 時,若函數
時,若函數![]() 的最小值為
的最小值為![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com