
【題目】如圖,在![]() 中,
中, ![]() 為直角,
為直角, ![]() .沿
.沿![]() 的中位線
的中位線![]() ,將平面
,將平面![]() 折起,使得
折起,使得![]() ,得到四棱錐
,得到四棱錐![]() .
.
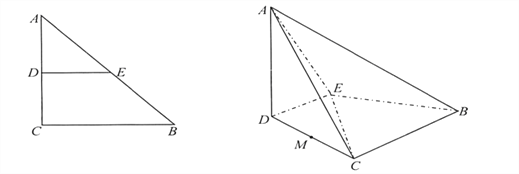
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求三棱錐![]() 的體積;
的體積;
(Ⅲ)![]() 是棱
是棱![]() 的中點,過
的中點,過![]() 做平面
做平面![]() 與平面
與平面![]() 平行,設平面
平行,設平面![]() 截四棱錐
截四棱錐![]() 所得截面面積為
所得截面面積為![]() ,試求
,試求![]() 的值.
的值.
【答案】(Ⅰ)見解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】【試題分析】(1)依據題設條件,借助線面垂直的判定定理分析推證;(2)先確定三棱錐的高,再運用三棱錐的體積公式求解;(3)先確定截面的位置,再分析探求截面的面積:
(Ⅰ)證明:因為![]() ,且
,且![]() ,
,
所以![]() ,同時
,同時![]() ,
,
又![]() ,所以
,所以![]() 面
面![]() .
.
又因為![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)可知: ![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() ,
,
又因為![]() ,所以
,所以![]() .
.
又因為![]() ,所以
,所以![]() 平面
平面![]() .
.
所以, ![]() .
.
依題意, ![]() .
.
所以, ![]() .
.
(Ⅲ)分別取![]() 的中點
的中點![]() ,并連接
,并連接![]() ,
,
因為平面![]() 平面
平面![]() ,所以平面
,所以平面![]() 與平面
與平面![]() 的交線平行于
的交線平行于![]() ,因為
,因為![]() 是中點,所以平面
是中點,所以平面![]() 與平面
與平面![]() 的交線是
的交線是![]() 的中位線
的中位線![]() .同理可證,四邊形
.同理可證,四邊形![]() 是平面
是平面![]() 截四棱錐
截四棱錐![]() 的截面.
的截面.
即: ![]() .
.
由(Ⅰ)可知: ![]() 平面
平面![]() ,所以
,所以![]() ,
,
又∵![]() ,
, ![]() ∴
∴![]() .
.
∴四邊形![]() 是直角梯形.
是直角梯形.
在![]() 中,
中, ![]() ∴
∴![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)某班主任對全班50名學生學習積極性和參加社團活動情況進行調查,統計數據如表1所示
表1
參加社團活動 | 不參加社團活動 | 合計 | |
學習積極性高 | 17 | 8 | 25 |
學習積極性一般 | 5 | 20 | 25 |
合計 | 22 | 28 | 50 |
(1)如果隨機從該班抽查一名學生,抽到參加社團活動的學生的概率是多少?抽到不參加社團活動且學習積極性一般的學生的概率是多少?
(2)運用獨立檢驗的思想方法分析:學生的學習積極性與參加社團活動情況是否有關系?并說明理由.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
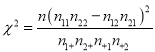
查看答案和解析>>
科目:高中數學 來源: 題型:
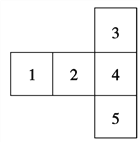
【題目】編號為A,B,C,D,E的5個小球放在如圖所示的5個盒子里,要求每個盒子只能放1個小球,且A球不能放在1,2號盒子里,B球必須放在與A球相鄰的盒子中,求不同的放法有多少種?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌汽車的![]() 店,對最近100份分期付款購車情況進行統計,統計情況如下表所示.已知分9期付款的頻率為0.4;該店經銷一輛該品牌汽車,若顧客分3期付款,其利潤為1萬元;分6期或9期付款,其利潤為2萬元;分12期付款,其利潤為3萬元.
店,對最近100份分期付款購車情況進行統計,統計情況如下表所示.已知分9期付款的頻率為0.4;該店經銷一輛該品牌汽車,若顧客分3期付款,其利潤為1萬元;分6期或9期付款,其利潤為2萬元;分12期付款,其利潤為3萬元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
頻數 | 20 | 20 |
|
|
(1)若以上表計算出的頻率近似替代概率,從該店采用分期付款購車的顧客(數量較大)中隨機抽取3為顧客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分層抽樣方式從這100為顧客中抽取5人,再從抽取的5人中隨機抽取3人,記該店在這3人身上賺取的總利潤為隨機變量![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,我海監船在![]() 島海域例行維權巡航,某時刻航行至
島海域例行維權巡航,某時刻航行至![]() 處,此時測得其東北方向與它相距
處,此時測得其東北方向與它相距![]() 海里的
海里的![]() 處有一外國船只,且
處有一外國船只,且![]() 島位于海監船正東
島位于海監船正東![]() 海里處.
海里處.
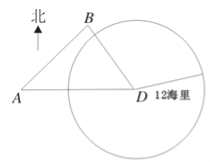
(1)求此時該外國船只與![]() 島的距離;
島的距離;
(2)觀測中發現,此外國船只正以每小時![]() 海里的速度沿正南方向航行,為了將該船攔截在離
海里的速度沿正南方向航行,為了將該船攔截在離![]() 島
島![]() 海里處,不讓其進入
海里處,不讓其進入![]() 島
島![]() 海里內的海域,試確定海監船的航向,并求其速度的最小值.(參考數據:
海里內的海域,試確定海監船的航向,并求其速度的最小值.(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的離心率為
)的離心率為![]() ,以橢圓的四個頂點為頂點的四邊形的面積為8.
,以橢圓的四個頂點為頂點的四邊形的面積為8.
(Ⅰ)求橢圓![]() 的方程;
的方程;
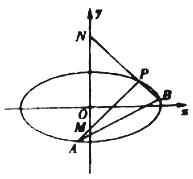
(Ⅱ)如圖,斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 的左上方.若
的左上方.若![]() ,且直線
,且直線![]() ,
, ![]() 分別與
分別與![]() 軸交于
軸交于![]() ,
, ![]() 點,求線段
點,求線段![]() 的長度.
的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com