選修4-4:極坐標系與參數(shù)方程
已知曲線C
1:
(t為參數(shù)),C
2:
(θ為參數(shù)).
(1)化C
1,C
2的方程為普通方程;
(2)若C
1上的點P對應(yīng)的參數(shù)為t=
,Q為C
2上的動點,求PQ中點M到直線C
3:
(t為參數(shù))距離的最小值.
(1)對于曲線C
1:
(t為參數(shù)),利用同角三角函數(shù)的基本關(guān)系消去參數(shù)t,可得 (x+4)
2+(y-3)
2=1;
對于曲線 C
2:
(θ為參數(shù)),利用同角三角函數(shù)的基本關(guān)系消去參數(shù)θ,可得
+
=1.
(2)若C
1上的點P對應(yīng)的參數(shù)為t=
,則點P的坐標為(-4,4),
設(shè)Q(8cosθ,3sinθ)為C
2上的動點,則PQ中點M( 4cosθ-2,
).
直線C
3:
(t為參數(shù)),即 x-2y-7=0.
∴點M到直線C
3:x-2y-7=0 的距離為 d=
=
=
,其中,sin∅=
,cos∅=-
.
故當sin(θ+∅)=1時,d取得最小值為
=
.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
在極坐標系中,直線ρcosθ=1與曲線ρ=4cosθ相交于A、B兩點,O為極點,則∠AOB的大小為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知點
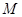
的直角坐標
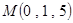
,則它的柱坐標為____;
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在平面直角坐標系xOy中,以O(shè)為極點,X軸的正半軸為極軸,取與直角坐標系相同的長度單位建立極坐標系.曲線C
1的參數(shù)方程為:
(φ為參數(shù));射線C
2的極坐標方程為:θ=
,且射線C
2與曲線C
1的交點的橫坐標為
(I)求曲線C
1的普通方程;
(II)設(shè)A、B為曲線C
1與y軸的兩個交點,M為曲線C
1上不同于A、B的任意一點,若直線AM與MB分別與x軸交于P,Q兩點,求證|OP|.|OQ|為定值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若直線y=x-b與曲線
(θ∈[0,2π))有兩個不同的公共點,則實數(shù)b的取值范圍為( ).
| A.(2-,1) | B.[2-,2+] |
| C.(-∞,2-)∪(2+,+∞) | D.(2-,2+) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
直線3x-4y-1=0被曲線
(θ為參數(shù))所截得的弦長為______.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知極坐標方程為ρcosθ+ρsinθ-1=0的直線與x軸的交點為P,與橢圓
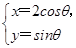
(θ為參數(shù))交于點A、B,求PA·PB的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
(坐標系與參數(shù)方程選做題)曲線C的極坐標方程
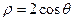
,直角坐標系中的點M的坐標為(0,2),P為曲線C上任意一點,則
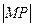
的最小值是
.
查看答案和解析>>



 的參數(shù)方程是( )
的參數(shù)方程是( ) (t為參數(shù))
(t為參數(shù))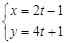 (t為參數(shù))
(t為參數(shù))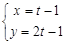 (t為參數(shù))
(t為參數(shù)) (
( 為參數(shù))
為參數(shù))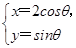 (θ為參數(shù))交于點A、B,求PA·PB的值.
(θ為參數(shù))交于點A、B,求PA·PB的值.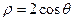 ,直角坐標系中的點M的坐標為(0,2),P為曲線C上任意一點,則
,直角坐標系中的點M的坐標為(0,2),P為曲線C上任意一點,則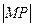 的最小值是 .
的最小值是 .