
【題目】如圖,已知長方形ABCD中,AB=2,AD=1,M為DC的中點(diǎn).將△ADM沿AM折起,使得平面ADM⊥平面ABCM,E為BD的中點(diǎn). 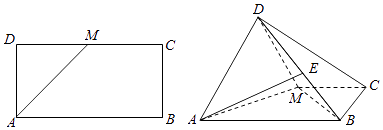
(1)求證:BM⊥平面ADM;
(2)求直線AE與平面ADM所成角的正弦值.
【答案】
(1)解:△ABM中,AB=2, ![]() ,∴AM⊥BM,
,∴AM⊥BM,
又平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,且BM平面ABCM,
∴BM⊥平面ADM
(2)解:如圖,以M點(diǎn)為坐標(biāo)原點(diǎn),MA所在直線為x軸,MB所在直線為y軸建立空間直角坐標(biāo)系,
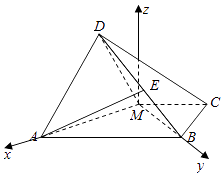
則M(0,0,0), ![]() ,
, ![]() ,
, ![]() ,
,
∵E為BD中點(diǎn),∴ ![]() ,
, ![]() ,
,
由(1)知, ![]() 為平面ADM的一個法向量,
為平面ADM的一個法向量,
![]() ,
,
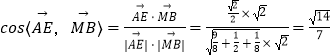 ,
,
∴直線AE與平面ADM所成角的正弦值為 ![]()
【解析】(1)根據(jù)線面垂直的判定定理證明即可;(2)求出平面ADM的一個法向量,求出 ![]() ,
, ![]() 的余弦值,從而求出直線AE與平面ADM所成角的正弦值.
的余弦值,從而求出直線AE與平面ADM所成角的正弦值.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(12分)
如圖,四棱錐P-ABCD中,側(cè)面PAD為等比三角形且垂直于底面ABCD,![]() E是PD的中點(diǎn).
E是PD的中點(diǎn).

(1)證明:直線![]() 平面PAB
平面PAB
(2)點(diǎn)M在棱PC 上,且直線BM與底面ABCD所成銳角為![]() ,求二面角M-AB-D的余弦值
,求二面角M-AB-D的余弦值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() (其中a為非零實(shí)數(shù)),且方程
(其中a為非零實(shí)數(shù)),且方程 ![]() 有且僅有一個實(shí)數(shù)根. (Ⅰ)求實(shí)數(shù)a的值;
有且僅有一個實(shí)數(shù)根. (Ⅰ)求實(shí)數(shù)a的值;
(Ⅱ)證明:函數(shù)f(x)在區(qū)間(0,+∞)上單調(diào)遞減.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】拖延癥總是表現(xiàn)在各種小事上,但日積月累,特別影響個人發(fā)展.某校的一個社會實(shí)踐調(diào)查小組,在對該校學(xué)生進(jìn)行“是否有明顯拖延癥”的調(diào)查中,隨機(jī)發(fā)放了110份問卷.對收回的100份有效問卷進(jìn)行統(tǒng)計(jì),得到如下![]() 列聯(lián)表:
列聯(lián)表:
有明顯拖延癥 | 無明顯拖延癥 | 合計(jì) | |
男 | 35 | 25 | 60 |
女 | 30 | 10 | 40 |
合計(jì) | 65 | 35 | 100 |
(Ⅰ)按女生是否有明顯拖延癥進(jìn)行分層,已經(jīng)從40份女生問卷中抽取了8份問卷,現(xiàn)從這8份問卷中再隨機(jī)抽取3份,并記其中無明顯拖延癥的問卷的份數(shù)為![]() ,試求隨機(jī)變量
,試求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(Ⅱ)若在犯錯誤的概率不超過![]() 的前提下認(rèn)為無明顯拖延癥與性別有關(guān),那么根據(jù)臨界值表,最精確的
的前提下認(rèn)為無明顯拖延癥與性別有關(guān),那么根據(jù)臨界值表,最精確的![]() 的值應(yīng)為多少?請說明理由.
的值應(yīng)為多少?請說明理由.
附:獨(dú)立性檢驗(yàn)統(tǒng)計(jì)量 ,其中
,其中![]() .
.
獨(dú)立性檢驗(yàn)臨界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
已知曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() ,以極點(diǎn)為原點(diǎn),極軸為
,以極點(diǎn)為原點(diǎn),極軸為![]() 軸的正半軸建立平面直角坐標(biāo)系,直線
軸的正半軸建立平面直角坐標(biāo)系,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)).
為參數(shù)).
(I)寫出直線![]() 的一般方程與曲線
的一般方程與曲線![]() 的直角坐標(biāo)方程,并判斷它們的位置關(guān)系;
的直角坐標(biāo)方程,并判斷它們的位置關(guān)系;
(II)將曲線![]() 向左平移
向左平移![]() 個單位長度,向上平移
個單位長度,向上平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]() ,設(shè)曲線
,設(shè)曲線![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換![]() 得到曲線
得到曲線![]() ,設(shè)曲線
,設(shè)曲線![]() 上任一點(diǎn)為
上任一點(diǎn)為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給定橢圓![]() ,稱圓心在原點(diǎn)
,稱圓心在原點(diǎn)![]() ,半徑為
,半徑為![]() 的圓是橢圓
的圓是橢圓![]() 的“準(zhǔn)圓”.若橢圓
的“準(zhǔn)圓”.若橢圓![]() 的一個焦點(diǎn)為
的一個焦點(diǎn)為![]() ,其短軸上的一個端點(diǎn)到
,其短軸上的一個端點(diǎn)到![]() 的距離為
的距離為![]() .
.

(1)求橢圓![]() 的方程和其“準(zhǔn)圓”方程;
的方程和其“準(zhǔn)圓”方程;
(2)點(diǎn)![]() 是橢圓
是橢圓![]() 的“準(zhǔn)圓”上的動點(diǎn),過點(diǎn)
的“準(zhǔn)圓”上的動點(diǎn),過點(diǎn)![]() 作橢圓的切線
作橢圓的切線![]() 交“準(zhǔn)圓”于點(diǎn)
交“準(zhǔn)圓”于點(diǎn)![]() .
.
①當(dāng)點(diǎn)![]() 為“準(zhǔn)圓”與
為“準(zhǔn)圓”與![]() 軸正半軸的交點(diǎn)時,求直線
軸正半軸的交點(diǎn)時,求直線![]() 的方程并證明
的方程并證明![]() ;
;
②求證:線段![]() 的長為定值.
的長為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】北京、張家港2022年冬奧會申辦委員會在俄羅斯索契舉辦了發(fā)布會,某公司為了競標(biāo)配套活動的相關(guān)代言,決定對旗下的某商品進(jìn)行一次評估.該商品原來每件售價為25元,年銷售8萬件.
(1)據(jù)市場調(diào)查,若價格每提高1元,銷售量將相應(yīng)減少2000件,要使銷售的總收入不低于原收入,該商品每件定價最多為多少元?
(2)為了抓住申奧契機(jī),擴(kuò)大該商品的影響力,提高年銷售量.公司決定立即對該商品進(jìn)行全面技術(shù)革新和營銷策略改革,并提高定價到x元.公司擬投入 ![]() 萬作為技改費(fèi)用,投入(50+2x)萬元作為宣傳費(fèi)用.試問:當(dāng)該商品改革后的銷售量a至少應(yīng)達(dá)到多少萬件時,才可能使改革后的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
萬作為技改費(fèi)用,投入(50+2x)萬元作為宣傳費(fèi)用.試問:當(dāng)該商品改革后的銷售量a至少應(yīng)達(dá)到多少萬件時,才可能使改革后的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在等差數(shù)列{an} 中,已知公差 ![]() ,且a1+a3+a5+…+a99=60,則a1+a2+a3+…+a100= .
,且a1+a3+a5+…+a99=60,則a1+a2+a3+…+a100= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】平面內(nèi)給定三個向量 ![]() =(3,2),
=(3,2), ![]() =(﹣1,2),
=(﹣1,2), ![]() =(4,1).回答下列問題:
=(4,1).回答下列問題:
(1)若( ![]() +k
+k ![]() )∥(2
)∥(2 ![]() ﹣
﹣ ![]() ),求實(shí)數(shù)k;
),求實(shí)數(shù)k;
(2)設(shè) ![]() =(x,y)滿足(
=(x,y)滿足( ![]() ﹣
﹣ ![]() )∥(
)∥( ![]() +
+ ![]() )且|
)且| ![]() ﹣
﹣ ![]() |=1,求
|=1,求 ![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com