
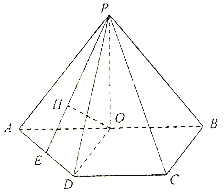
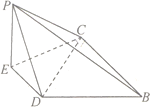
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中點,
的中點,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影為點
上的正投影為點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() 為
為![]() 中點;
中點;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上確定一點
上確定一點![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 與面
與面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析(2)![]()
【解析】試題分析:
(1)連接OE,可得四邊形BCDO是平行四邊形,由PO⊥底面ABCD.O在平面PAD上的正投影為點H,可得AD⊥OE,又AO=OD,即可得E為AD中點;(2)以O為原點建立空間直角坐標系,設![]() ,∴
,∴![]() ,∴
,∴![]() ,又
,又![]() 是平面PAB的法向量,求出面PCD的法向量,即可求得OG與面PCD所成角的正弦值.
是平面PAB的法向量,求出面PCD的法向量,即可求得OG與面PCD所成角的正弦值.
詳解:(1)連結![]() ,∵
,∵![]() ,
,![]() 是
是![]() 中點,
中點,![]() ,
,

∴![]() ,∵
,∵![]() ,∴四邊形
,∴四邊形![]() 是平行四邊形,∴
是平行四邊形,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() 在平面
在平面![]() 的正投影為
的正投影為![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 是
是![]() 的中點.
的中點.
(2)∵![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的正方向建立空間直角坐標系
的正方向建立空間直角坐標系![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() 是
是![]() 的外心,∵
的外心,∵![]() ,
,
∴![]() 是
是![]() 的重心,∴
的重心,∴![]() ,
,
設![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() 是平面
是平面![]() 的一個法向量,且
的一個法向量,且![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
設![]() 是平面
是平面![]() 的法向量,∵
的法向量,∵![]() ,
,![]() ,
,
∴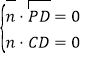 ,即
,即![]() ,取
,取![]() ,則
,則![]() ,
,![]() ,∴
,∴![]()
∴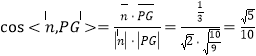 ,∴直線
,∴直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() ,如圖1.以
,如圖1.以![]() 為折痕將
為折痕將![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,如圖2.
的位置,如圖2.
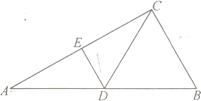
如圖1 如圖2
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,過點
,過點![]() 作與
作與![]() 軸平行的直線
軸平行的直線![]() ,點
,點![]() 為動點
為動點![]() 在直線
在直線![]() 上的投影,且滿足
上的投影,且滿足![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知點![]() 為曲線
為曲線![]() 上的一點,且曲線
上的一點,且曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,若
,若![]() 與直線
與直線![]() 相交于點
相交于點![]() ,試探究在
,試探究在![]() 軸上是否存在點
軸上是否存在點![]() ,使得以
,使得以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某玩具廠生產出一種新型兒童泡沫玩具飛機,為更精確的確定最終售價,該廠采用了多種價格對該玩具飛機進行了試銷,某銷售點的銷售情況如下表:
單價 | 8 | 9 | 10 | 11 | 12 |
銷量 | 40 | 36 | 30 | 24 | 20 |
從散點圖可以看出,這些點大致分布在一條直線的附近,變量![]() ,
,![]() 有較強的線性相關性.
有較強的線性相關性.
(1)求銷量![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)若每架該玩具飛機的成本價為5元,利用(1)的結果,預測每架該玩具飛機的定價為多少元時,總利潤最大.(結果保留一位小數)
(附: ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某客戶準備在家中安裝一套凈水系統,該系統為三級過濾,使用壽命為十年.如圖所示,兩個一級過濾器采用并聯安裝,二級過濾器與三級過濾器為串聯安裝。

其中每一級過濾都由核心部件濾芯來實現。在使用過程中,一級濾芯和二級濾芯都需要不定期更換(每個濾芯是否需要更換相互獨立),三級濾芯無需更換,若客戶在安裝凈水系統的同時購買濾芯,則一級濾芯每個![]() 元,二級濾芯每個
元,二級濾芯每個![]() 元.若客戶在使用過程中單獨購買濾芯,則一級濾芯每個
元.若客戶在使用過程中單獨購買濾芯,則一級濾芯每個![]() 元,二級濾芯每個
元,二級濾芯每個![]() 元。現需決策安裝凈水系統的同時購濾芯的數量,為此參考了根據
元。現需決策安裝凈水系統的同時購濾芯的數量,為此參考了根據![]() 套該款凈水系統在十年使用期內更換濾芯的相關數據制成的圖表,其中圖是根據
套該款凈水系統在十年使用期內更換濾芯的相關數據制成的圖表,其中圖是根據![]() 個一級過濾器更換的濾芯個數制成的柱狀圖,表是根據
個一級過濾器更換的濾芯個數制成的柱狀圖,表是根據![]() 個二級過濾器更換的濾芯個數制成的頻數分布表.
個二級過濾器更換的濾芯個數制成的頻數分布表.

二級濾芯更換頻數分布表
二級濾芯更換的個數 |
|
|
頻數 |
|
|
以![]() 個一級過濾器更換濾芯的頻率代替
個一級過濾器更換濾芯的頻率代替![]() 個一級過濾器更換濾芯發生的概率,以
個一級過濾器更換濾芯發生的概率,以![]() 個二級過濾器更換濾芯的頻率代替
個二級過濾器更換濾芯的頻率代替![]() 個二級過濾器更換濾芯發生的概率.
個二級過濾器更換濾芯發生的概率.
(1)求一套凈水系統在使用期內需要更換的各級濾芯總個數恰好為![]() 的概率;
的概率;
(2)記![]() 表示該客戶的凈水系統在使用期內需要更換的一級濾芯總數,求
表示該客戶的凈水系統在使用期內需要更換的一級濾芯總數,求![]() 的分布列及數學期望;
的分布列及數學期望;
(3)記![]() ,
,![]() 分別表示該客戶在安裝凈水系統的同時購買的一級濾芯和二級濾芯的個數.若
分別表示該客戶在安裝凈水系統的同時購買的一級濾芯和二級濾芯的個數.若![]() ,且
,且![]() ,以該客戶的凈水系統在使用期內購買各級濾芯所需總費用的期望值為決策依據,試確定
,以該客戶的凈水系統在使用期內購買各級濾芯所需總費用的期望值為決策依據,試確定![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知以點C![]() (t∈R,t≠0)為圓心的圓與x軸交于點O和點A,與y軸交于點O和點B,其中O為原點.
(t∈R,t≠0)為圓心的圓與x軸交于點O和點A,與y軸交于點O和點B,其中O為原點.
(1)求證:△OAB的面積為定值;
(2)設直線y=-2x+4與圓C交于點M,N,若OM=ON,求圓C的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的右頂點到其一條漸近線的距離等于
的右頂點到其一條漸近線的距離等于![]() ,拋物線
,拋物線![]() 的焦點與雙曲線
的焦點與雙曲線![]() 的右焦點重合,則拋物線
的右焦點重合,則拋物線![]() 上的動點
上的動點![]() 到直線
到直線![]() 和
和![]() 距離之和的最小值為( )
距離之和的最小值為( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com