
【題目】命題![]() :已知實數
:已知實數![]() ,
, ![]() 滿足約束條件
滿足約束條件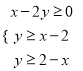 ,二元一次不等式
,二元一次不等式![]() 恒成立,
恒成立,
命題![]() :設數列
:設數列![]() 的通項公式為
的通項公式為![]() ,若
,若![]() ,使得
,使得![]() .
.
(1)分別求出使命題![]() ,
, ![]() 為真時,實數
為真時,實數![]() 的取值范圍;
的取值范圍;
(2)若命題![]() 與
與![]() 真假相同,求實數
真假相同,求實數![]() 的取值范圍.
的取值范圍.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,正四棱錐P﹣ABCD中,側棱PA與底面ABCD所成的角的正切值為![]() .
.
(1)求側面PAD與底面ABCD所成的二面角的大小;
(2)若E是PB的中點,求異面直線PD與AE所成角的正切值;
(3)問在棱AD上是否存在一點F,使EF⊥側面PBC,若存在,試確定點F的位置;若不存在,說明理由.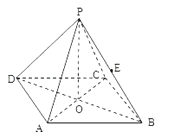
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2mx+m2+4m﹣2.
(1)若函數f(x)在區間[0,1]上是單調遞減函數,求實數m的取值范圍;
(2)若函數f(x)在區間[0,1]上有最小值﹣3,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某紡紗廠生產甲、乙兩種棉紗,已知生產甲種棉紗1噸需耗一級籽棉2噸、二級籽棉1噸;生產乙種棉紗1噸需耗一級籽棉1噸,二級籽棉2噸.每1噸甲種棉紗的利潤為900元,每1噸乙種棉紗的利潤為600元.工廠在生產這兩種棉紗的計劃中,要求消耗一級籽棉不超過250噸,二級籽棉不超過300噸.問甲、乙兩種棉紗應各生產多少噸,能使利潤總額最大?并求出利潤總額的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正△ABC三個頂點都在半徑為2的球面上,球心O到平面ABC的距離為1,點E是線段AB的中點,過點E作球O的截面,則截面面積的最小值是( )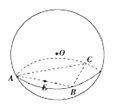
A.![]()
B.2π
C.![]()
D.3π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 (本小題滿分12分)
如圖, 在四面體ABOC中, ![]() , 且
, 且![]() .
.
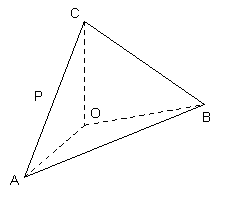
(Ⅰ)設為![]() 為
為![]() 的中點, 證明: 在
的中點, 證明: 在![]() 上存在一點
上存在一點![]() ,使
,使![]() ,并計算
,并計算![]() ;
;
(Ⅱ)求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位用2160萬元購得一塊空地,計劃在該地塊上建造一棟至少10層,每層2000平方米的樓房.經測算,如果將樓房建為x(x≥10)層,則每平方米的平均建筑費用為560+48x(單位:元).
(1)寫出樓房平均綜合費用y關于建造層數x的函數關系式;
(2)該樓房應建造多少層時,可使樓房每平方米的平均綜合費用最少?最少值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值![]() ,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出
,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出![]() 的值為 ( )
的值為 ( )
(參考數據:![]() )
)
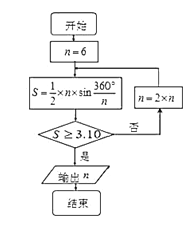
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面α過正方體ABCD﹣A1B1C1D1的頂點A,α∥平面CB1D1 , α∩平面ABCD=m,α∩平面AB B1A1=n,則m,n所成角的正弦值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com