
【題目】已知函數![]() ,其中
,其中![]() ,且
,且![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)設![]() ,若
,若![]() 存在極大值,且對于
存在極大值,且對于![]() 的一切可能取值,
的一切可能取值, ![]() 的極大值均小于
的極大值均小于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;(2)
;(2)![]()
【解析】試題分析:
(1)計算出導數![]() ,由不等式
,由不等式![]() 得增區間,由
得增區間,由![]() 得減區間,注意要按
得減區間,注意要按![]() 的正負分類討論,
的正負分類討論, ![]() 的正負對定義域有影響;
的正負對定義域有影響;
(2)求出導數![]() ,因此必須有
,因此必須有![]() ,
, ![]() 才能有兩個不等實根,
才能有兩個不等實根, ![]() 的兩實根為
的兩實根為![]() ,
, ![]() ,極大值為
,極大值為![]() ,由求根公式得
,由求根公式得![]() ,令
,令![]() (作為
(作為![]() 的函數),同理由導數知識得
的函數),同理由導數知識得![]() 在
在![]() 上單調遞減,從而
上單調遞減,從而![]() ,由
,由![]() 可得
可得![]() 的范圍.
的范圍.
試題解析:
(1) ![]() 時,
時, ![]() ,故
,故![]()
當![]() 時,
時, ![]() ,由
,由![]() ,得
,得![]() 得
得![]()
因此![]() 的單調遞增區間為:
的單調遞增區間為: ![]() ,單調遞減區間為:
,單調遞減區間為: ![]()
當![]() 時,
時, ![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]()
因此單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]()
(2)由題![]() ,顯然
,顯然![]() ,設
,設![]() 的兩根為
的兩根為![]() ,則當
,則當![]() 或
或![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,故
,故![]() 極大
極大![]() 只可能是
只可能是![]() ,且
,且![]() ,知
,知![]() ,又
,又![]() ,故
,故![]() ,且
,且![]() ,
,
從而![]() 令
令![]() ,
,
則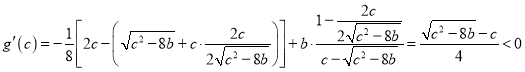 ,
,
故![]() 在
在![]() 單減,從而
單減,從而![]() ,
,
因此![]() ,解得
,解得![]()


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:高中數學 來源: 題型:
【題目】計算
(1)計算27 ![]() +lg5﹣2log23+lg2+log29.
+lg5﹣2log23+lg2+log29.
(2)已知f(x)=3x2﹣5x+2,求f( ![]() )、f(﹣a)、f(a+3).
)、f(﹣a)、f(a+3).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年10月28日,經歷了近半個世紀風雨的南京長江大橋真“累”了,終于停下來喘口氣了,之前大橋在改善我們城市的交通狀況方面功不可沒.據相關數據統計,一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米)的函數.當橋上的車流密度達到280輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過30輛/千米時,車流速度為50千米/小時.研究表明,當30≤x≤280時,車流速度v是車流密度x的一次函數.
(1)當0≤x≤280時,求函數v(x)的表達式;
(2)當車流密度x為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時) f(x)=xv(x)可以達到最大,并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某輛汽車以x km/h的速度在高速公路上勻速行駛(考慮到高速公路行車安全要求60≤x≤120)時,每小時的油耗(所需要的汽油量)為![]() ,其中k為常數,若汽車以120km/h的速度行駛時,每小時的油耗為11.5L.
,其中k為常數,若汽車以120km/h的速度行駛時,每小時的油耗為11.5L.
(1)求k的值;
(2)求該汽車每小時油耗的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知不等式ax2+5x+b>0的解集是{x|2<x<3},則不等式bx2﹣5x+a>0的解集是( )
A.{x|x<﹣3或x>﹣2}
B.{x|x<﹣ ![]() 或x>﹣
或x>﹣ ![]() }
}
C.{x|﹣ ![]() <x<﹣
<x<﹣ ![]() }
}
D.{x|﹣3<x<﹣2}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),a>0,且a≠1.
(1)若1是關于x的方程f(x)﹣g(x)=0的一個解,求t的值;
(2)當0<a<1且t=﹣1時,解不等式f(x)≤g(x);
(3)若函數F(x)=af(x)+tx2﹣2t+1在區間(﹣1,2]上有零點,求t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(﹣4,4)、B(4,4),直線AM與BM相交于點M,且直線AM的斜率與直線BM的斜率之差為﹣2,點M的軌跡為曲線C.
(1)求曲線C 的軌跡方程;
(2)Q為直線y=﹣1上的動點,過Q做曲線C的切線,切點分別為D、E,求△QDE的面積S的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com