【題目】如圖，在四棱錐
中， 
為等邊三角形，平面
平面
， 
， 
， 
， 
， 
為
的中點．
（
）求證： 
．
（
）求二面角
的余弦值．
（
）若
平面
，求
的值．
【答案】（1）見解析；（2）余弦為
；（2）
.
【解析】試題分析：（1）要證
，可以先證明
垂直于
所在的平面
；（2）可以用向量法解決，取
的中點
，連接
，以
為原點，分別以
為
軸建立空間直角坐標系，分別求出兩平面
、平面
的法向量，并求出法向量的夾角的余弦值，進而得到二面角
的余弦值；（3）因為
平面
，只需
，利用
即可求出
的值.
試題解析：（1）由于平面
平面
， 
為等邊三角形， 
為
的中點，則
，根據面面垂直性質定理，所以
平面
，又
平面
，則
．
（2）取
的中點
，連接
，以
為原點，分別以
為
軸建立空間直角坐標系，
，由于平面
與
軸垂直，則設平面
的法向量為
，設平面
的法向量
，則
，二面角
的余弦值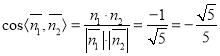
，由二面角
為鈍二面角，所以二面角
的斜弦值為
．
（3）有（1）知
平面
，則
，若
平面
，只需
，
，又
，解得
或
，由于
，則
．
培優三好生系列答案
優化作業上海科技文獻出版社系列答案科目：高中數學 來源： 題型：
【題目】給出下列四個命題：①若
，則
；②若，則
；③若，則
；④若
， 
且
，則
的最小值為9；其中正確命題的序號是______（將你認為正確的命題序號都填上）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，已知圓 
的圓心 
，半徑 
.
（1）求圓 的極坐標方程；
（2）若 
，直線 
的參數方程為 
為參數），直線 交圓 于 
兩點，求弦長 
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的公差d≠0，它的前n項和為Sn，若S5＝70，且a2，a7，a22成等比數列．
(1)求數列{an}的通項公式；
(2)設數列
的前n項和為Tn，求證： 
≤Tn＜
.
查看答案和解析>>
科目：高中數學 來源： 題型：
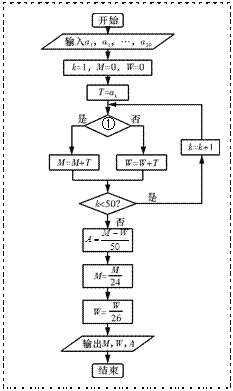
【題目】在一次“漢馬”（武漢馬拉松比賽的簡稱）全程比賽中，50名參賽選手（24名男選手和26名女選手）的成績（單位：分鐘）分別為數據
(成績不為0).
（Ⅰ）24名男選手成績的莖葉圖如圖⑴所示，若將男選手成績由好到差編為1～24號，再用系統抽樣方法從中抽取6人，求其中成績在區間
上的選手人數；
（Ⅱ）如圖⑵所示的程序用來對這50名選手的成績進行統計.為了便于區別性別，輸入時，男選手的成績數據用正數，女選手的成績數據用其相反數(負數)，請完成圖⑵中空白的判斷框①處的填寫，并說明輸出數值
和
的統計意義.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
為拋物線
： 
的焦點，點
為拋物線
上一定點。
（1）直線
過點
交拋物線
于
、
兩點，若
，求直線
的方程；
（2）過點
作兩條傾斜角互補的直線分別交拋物線
于異于點
的兩點
，試證明直線
的斜率為定值，并求出該定值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（14分）關于x的不等式ax2+（a﹣2）x﹣2≥0（a∈R）
（1）已知不等式的解集為（﹣∞，﹣1]∪[2，+∞），求a的值；
（2）解關于x的不等式ax2+（a﹣2）x﹣2≥0．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
