
【題目】已知拋物線C:y2=2x的焦點為F,過焦點F的直線交拋物線于A,B兩點,過A,B作準線的垂線交準線與P,Q兩點.R是PQ的中點.
(1)證明:以PQ為直徑的圓恒過定點F.
(2)證明:AR∥FQ.
【答案】(1)證明見解析(2)證明見解析
【解析】
(1)求得拋物線的焦點F,設直線l的方程為x=my+![]() ,聯立拋物線方程,設A(
,聯立拋物線方程,設A(![]() ,y1),B(
,y1),B(![]() ,y2),運用韋達定理,求得拋物線的準線方程,可得P,Q,R的坐標,
,y2),運用韋達定理,求得拋物線的準線方程,可得P,Q,R的坐標,
求得![]() ,
,![]() ,由向量垂直的條件,即可得證;
,由向量垂直的條件,即可得證;
(2)設AR的斜率為k1,FQ的斜率為k2,運用直線的斜率公式和兩直線平行的條件,以及韋達定理,即可得證.
證明:(1)拋物線C:y2=2x的焦點F(![]() ,0),設直線l的方程為x=my+
,0),設直線l的方程為x=my+![]() ,
,
聯立拋物線方程可得y2-2my-1=0,
設A(![]() ,y1),B(
,y1),B(![]() ,y2),則y1+y2=2m,y1y2=-1,
,y2),則y1+y2=2m,y1y2=-1,
拋物線的準線方程為x=-![]() ,可得P(-
,可得P(-![]() ,y1),Q(-
,y1),Q(-![]() ,y2),R(-
,y2),R(-![]() ,
,![]() ),
),
則![]() =(1,-y1),
=(1,-y1),![]() =(1,-y2),可得
=(1,-y2),可得![]()
![]() =1+y1y2=1-1=0,
=1+y1y2=1-1=0,
即PF⊥QF,以PQ為直徑的圓恒過定點F;
(2)設AR的斜率為k1,FQ的斜率為k2,
則k2=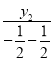 =-y2,
=-y2,
k1=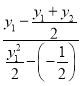 =
=![]() =
=![]() =
=![]() =-y2,
=-y2,
即k1=k2,
則AR∥FQ.


科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,常數
,常數![]() ).
).
(1)當![]() 時,討論函數
時,討論函數![]() 的奇偶性并說明理由;
的奇偶性并說明理由;
(2)若函數![]() 在區間
在區間![]() 上單調,求正數
上單調,求正數![]() 的取值范圍;
的取值范圍;
(3)若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為創建全國衛生城市,引入某公司的智能垃圾處理設備.已知每臺設備每月固定維護成本![]() 萬元,每處理一萬噸垃圾需增加
萬元,每處理一萬噸垃圾需增加![]() 萬元維護費用,每月處理垃圾帶來的總收益
萬元維護費用,每月處理垃圾帶來的總收益![]() 萬元與每月垃圾處理量
萬元與每月垃圾處理量![]() (萬噸)滿足關系:
(萬噸)滿足關系: (注:總收益=總成本+利潤)
(注:總收益=總成本+利潤)
(1)寫出每臺設備每月處理垃圾獲得的利潤![]() 關于每月垃圾處理量
關于每月垃圾處理量![]() 的函數關系;
的函數關系;
(2)該市計劃引入![]() 臺這種設備,當每臺每月垃圾處理量為何值時,所獲利潤最大?并求出最大利潤.
臺這種設備,當每臺每月垃圾處理量為何值時,所獲利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(
,(![]() 為常數)
為常數)
(1)若![]()
①求函數![]() 在區間
在區間![]() 上的最大值及最小值。
上的最大值及最小值。
②若過點![]() 可作函數
可作函數![]() 的三條不同的切線,求實數
的三條不同的切線,求實數![]() 的取值范圍。
的取值范圍。
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區某農產品近幾年的產量統計如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼t | 1 | 2 | 3 | 4 | 5 | 6 |
年產量y(萬噸) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根據表中數據,建立![]() 關于的線性回歸方程
關于的線性回歸方程![]() ;
;
(Ⅱ)根據線性回歸方程預測2019年該地區該農產品的年產量.
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: ,
,![]() .(參考數據:
.(參考數據:![]() ,計算結果保留小數點后兩位)
,計算結果保留小數點后兩位)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中點,E是PB中點.
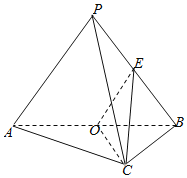
(1)證明:平面PAB⊥平面ABC;
(2)求點B到平面OEC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線方程為![]() ,其中
,其中![]()
(1)求證:直線恒過定點;
(2)當![]() 變化時,求點
變化時,求點![]() 到直線的距離的最大值;
到直線的距離的最大值;
(3)若直線分別與![]() 軸、
軸、![]() 軸的負半軸交于
軸的負半軸交于![]() 兩點,求
兩點,求![]() 面積的最小值及此時的直線方程.
面積的最小值及此時的直線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com