
【題目】設數列![]() 的前
的前![]() 項和
項和![]() ,已知
,已知![]() ,
,![]() .
.
(1)求證:數列![]() 為等差數列,并求出其通項公式;
為等差數列,并求出其通項公式;
(2)設![]() ,又
,又![]() 對一切
對一切![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)已知![]() 為正整數且
為正整數且![]() ,數列
,數列![]() 共有
共有![]() 項,設
項,設![]() ,又
,又![]() ,求
,求![]() 的所有可能取值.
的所有可能取值.
【答案】(1)證明見解析;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)當![]() 時,由所給的遞推關系式進行作差變形證明后項與前項之差為常數即可證得數列為等差數列,進一步可得數列的通項公式;
時,由所給的遞推關系式進行作差變形證明后項與前項之差為常數即可證得數列為等差數列,進一步可得數列的通項公式;
(2)結合(1)中的通項公式裂項求和,然后結合題意可確定實數![]() 的取值范圍;
的取值范圍;
(3)首先確定數列![]() 為等差數列,然后結合數列的單調性確定絕對值符號進行求和,得到關于k的不等式,最后求解關于k的不等式即可確定實數
為等差數列,然后結合數列的單調性確定絕對值符號進行求和,得到關于k的不等式,最后求解關于k的不等式即可確定實數![]() 的所有可能取值.
的所有可能取值.
(1)當![]() 時,
時,![]() ,
,![]() ,
,
兩式作差得![]() ,
,
故![]() ,
,
所以數列![]() 是公差為6的等差數列,
是公差為6的等差數列,
又![]() ,
,
所以![]() ;
;
(2)由于![]() ,故
,故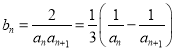 .
.
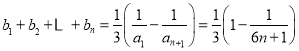 ,
,
顯然![]() 單調遞增,且
單調遞增,且![]() ,
,
故![]() , 所以
, 所以![]() .
.
(3)![]() ,則
,則![]() 是公差為
是公差為![]() 的等差數列,
的等差數列,
故當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ,
,
設數列![]() 的前n項和為
的前n項和為![]() ,于是:
,于是:
![]()
![]() ,
,
注意到![]() ,則
,則![]() ,題中的不等式即
,題中的不等式即![]() ,
,
所以![]() ,
,
所以,![]() 的所有可取值為
的所有可取值為![]() .
.


科目:高中數學 來源: 題型:
【題目】在測量一根新彈簧的勁度系數時,測得了如下的結果:
所掛重量( | 1 | 2 | 3 | 5 | 7 | 9 |
彈簧長度( | 11 | 12 | 12 | 13 | 14 | 16 |
(1)請在下圖坐標系中畫出上表所給數據的散點圖;

(2)若彈簧長度與所掛物體重量之間的關系具有線性相關性,請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程![]() ;
;
(3)根據回歸方程,求掛重量為![]() 的物體時彈簧的長度.所求得的長度是彈簧的實際長度嗎?為什么?
的物體時彈簧的長度.所求得的長度是彈簧的實際長度嗎?為什么?
注:本題中的計算結果保留小數點后兩位.
(參考公式: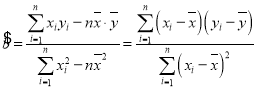 ,
,![]() )
)
(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() 與直線
與直線![]() :
:![]() ,動直線
,動直線![]() 過定點
過定點![]() .
.

(1)若直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 、
、![]() 兩點,點M是PQ的中點,直線
兩點,點M是PQ的中點,直線![]() 與直線
與直線![]() 相交于點N.探索
相交于點N.探索![]() 是否為定值,若是,求出該定值;若不是,請說明理由.
是否為定值,若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學成就的杰出代表作,其中《方田》章給出計算弧田面積所用的經驗方式為:弧田面積=![]() ,弧田(如圖)由圓弧和其所對弦所圍成,公式中“弦”指圓弧所對弦長,“矢”指半徑長與圓心到弦的距離之差。現有圓心角為
,弧田(如圖)由圓弧和其所對弦所圍成,公式中“弦”指圓弧所對弦長,“矢”指半徑長與圓心到弦的距離之差。現有圓心角為![]() ,半徑等于4米的弧田.下列說法不正確的是( )
,半徑等于4米的弧田.下列說法不正確的是( )

A. “弦”![]() 米,“矢”
米,“矢”![]() 米
米
B. 按照經驗公式計算所得弧田面積(![]() )平方米
)平方米
C. 按照弓形的面積計算實際面積為(![]() )平方米
)平方米
D. 按照經驗公式計算所得弧田面積比實際面積少算了大約0.9平方米(參考數據![]()
![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() 滿足:①對一切
滿足:①對一切![]() 恒有
恒有![]() ;②對一切
;②對一切![]() 恒有
恒有![]() ;③當
;③當![]() 時,
時,![]() ,且
,且![]() ;④若對一切
;④若對一切![]() (其中
(其中![]() ),不等式
),不等式![]() 恒成立.
恒成立.
(1)求![]() 的值;
的值;
(2)證明:函數![]() 是
是![]() 上的遞增函數;
上的遞增函數;
(3)求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() 中,底面
中,底面![]() 為矩形,且
為矩形,且![]() ,
,![]() ,若
,若![]() 平面
平面![]() ,
,![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點.
的中點.
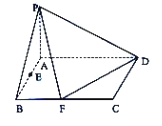
(1)證明:![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,確定點
?若存在,確定點![]() 的位置:若不存在,說明理由;
的位置:若不存在,說明理由;
(3)若![]() 與平面
與平面![]() 所成的角為45°,求二面角
所成的角為45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個孩子的身高![]() 與年齡
與年齡![]() (周歲)具有相關關系,根據所采集的數據得到線性回歸方程
(周歲)具有相關關系,根據所采集的數據得到線性回歸方程![]() ,則下列說法錯誤的是( )
,則下列說法錯誤的是( )
A.回歸直線一定經過樣本點中心![]()
B.斜率的估計值等于6.217,說明年齡每增加一個單位,身高就約增加6.217個單位
C.年齡為10時,求得身高是![]() ,所以這名孩子的身高一定是
,所以這名孩子的身高一定是![]()
D.身高與年齡成正相關關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的右頂點到其一條漸近線的距離等于
的右頂點到其一條漸近線的距離等于![]() ,拋物線
,拋物線![]() 的焦點與雙曲線
的焦點與雙曲線![]() 的右焦點重合,則拋物線
的右焦點重合,則拋物線![]() 上的動點
上的動點![]() 到直線
到直線![]() 和
和![]() 的距離之和的最小值為__________.
的距離之和的最小值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com