【題目】下列事件是隨機事件的是（ ）
①當x>10時，
； ②當x∈R，x2+x＝0有解
③當a∈R關于x的方程x2+a＝0在實數集內有解； ④當sinα>sinβ時，α>β（ ）
A.①②B.②③C.③④D.①④
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
(a>b>0)經過點(
，1)，以原點為圓心、橢圓短半軸長為半徑的圓經過橢圓的焦點．
(Ⅰ)求橢圓C的方程；
(Ⅱ)設過點(－1,0)的直線l與橢圓C相交于A，B兩點，試問在x軸上是否存在一個定點M，使得
恒為定值？若存在，求出該定值及點M的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對函數f(x)＝xsinx，現有下列命題：①函數f(x)是偶函數；②函數f(x)的最小正周期是2π；③點(π，0)是函數f(x)的圖象的一個對稱中心；④函數f(x)在區間
上單調遞增，在區間
上單調遞減．其中是真命題的是________．(寫出所有真命題的序號)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】汽車是碳排放量比較大的交通工具,某地規定,從2017年開始,將對二氧化碳排放量超過130 g/km的輕型汽車進行懲罰性征稅,檢測單位對甲、乙兩品牌輕型汽車各抽取5輛進行二氧化碳排放量檢測,記錄如下(單位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | 100 | 160 |
經測算得乙品牌輕型汽車二氧化碳排放量的平均值為
=120 g/km.
(1)求表中x的值,并比較甲、乙兩品牌輕型汽車二氧化碳排放量的穩定性;
(2)從被檢測的5輛甲品牌輕型汽車中任取2輛,則至少有一輛二氧化碳排放量超過130 g/km的概率是多少?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2018屆安徽省合肥市高三第一次教學質量檢測】一家大型購物商場委托某機構調查該商場的顧客使用移動支付的情況.調查人員從年齡在
內的顧客中，隨機抽取了180人，調查結果如表：
（1）為推廣移動支付，商場準備對使用移動支付的顧客贈送1個環保購物袋.若某日該商場預計有12000人購物，試根據上述數據估計，該商場當天應準備多少個環保購物袋？
（2）某機構從被調查的使用移動支付的顧客中，按分層抽樣的方式抽取7人作跟蹤調查，并給其中2人贈送額外禮品，求獲得額外禮品的2人年齡都在
內的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了迎接第二屆國際互聯網大會，組委會對報名參加服務的
名志愿者進行互聯網知識測試，從這
名志愿者中采用隨機抽樣的方法抽取
人，所得成績如下： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
.
（1）作出抽取的
人的測試成績的莖葉圖，以頻率為概率，估計這
志愿者中成績不低于
分的人數；
（2）從抽取的成績不低于
分的志愿者中，隨機選
名參加某項活動，求選取的
人恰有一人成績不低于
分的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某圖書公司有一款圖書的歷史收益率（收益率=利潤÷每本收入）的頻率分布直方圖如圖所示：
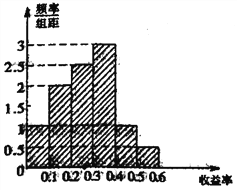
（1）試估計平均收益率；（用區間中點值代替每一組的數值）
（2）根據經驗，若每本圖書的收入在20元的基礎上每增加
元，對應的銷量
（萬份）與
（元）有較強線性相關關系，從歷史銷售記錄中抽樣得到如下5組
與
的對應數據：
據此計算出的回歸方程為
①求參數
的估計值；
②若把回歸方程
當作
與
的線性關系， 
取何值時，此產品獲得最大收益，并求出該最大收益.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
