
【題目】已知數列{an}滿足:a1= ![]() ,an+1=
,an+1= ![]() (n∈N*).
(n∈N*).
(1)求a2 , a3的值;
(2)證明:不等式0<an<an+1對于任意n∈N*都成立.
科目:高中數學 來源: 題型:
【題目】端午節吃粽子是我國的傳統習俗,設一盤中裝有![]() 個粽子,其中豆沙粽
個粽子,其中豆沙粽![]() 個,肉粽
個,肉粽![]() 個,白粽
個,白粽![]() 個,這三種粽子的外觀完全相同,從中任意選取
個,這三種粽子的外觀完全相同,從中任意選取![]() 個.
個.
(![]() )求三種粽子各取到
)求三種粽子各取到![]() 個的概率.
個的概率.
(![]() )設
)設![]() 表示取到的豆沙粽個數,求
表示取到的豆沙粽個數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是兩個獨立的轉盤(A)、(B),在兩個圖中三個扇形區域的圓心角分別為60°、120°、180°.用這兩個轉盤進行游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤(A)指針所對的區域為x,轉盤(B)指針所對的區域為y,x、y∈{1,2,3},設x+y的值為ξ. 
(1)求x<2且y>1的概率;
(2)求隨機變量ξ的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cos2x﹣sin2xsinφ﹣2cos2xsin2 ![]() (0<φ<
(0<φ< ![]() )的圖象的一個對稱中心為(
)的圖象的一個對稱中心為( ![]() ,0),則下列說法不正確的是( )
,0),則下列說法不正確的是( )
A.直線x= ![]() π是函數f(x)的圖象的一條對稱軸
π是函數f(x)的圖象的一條對稱軸
B.函數f(x)在[0, ![]() ]上單調遞減
]上單調遞減
C.函數f(x)的圖象向右平移 ![]() 個單位可得到y=cos2x的圖象
個單位可得到y=cos2x的圖象
D.函數f(x)在x∈[0, ![]() ]上的最小值為﹣1
]上的最小值為﹣1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是R上的偶函數,且在區間(﹣∞,0)是單調遞增的,若S1= ![]() x2dx,S2=
x2dx,S2= ![]()
![]() dx,S3=
dx,S3= ![]() exdx,則f(S1),f(S2),f(S3)的大小關系是 .
exdx,則f(S1),f(S2),f(S3)的大小關系是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地有三家工廠,分別位于矩形ABCD 的頂點A、B 及CD的中點P 處,已知AB=20km,CB =10km ,為了處理三家工廠的污水,現要在矩形ABCD 的區域上(含邊界),且與A、B等距離的一點O處建造一個污水處理廠,并鋪設排污管道AO、BO、OP ,設排污管道的總長度為![]() km.
km.
(1)按下列要求寫出函數關系式:①設∠BAO= ![]() (rad),將
(rad),將![]() 表示成
表示成![]() 的函數;②設OP
的函數;②設OP ![]() (km) ,將
(km) ,將![]() 表示成
表示成![]() 的函數.
的函數.
(2)請選用(1)中的一個函數關系式,確定污水處理廠的位置,使鋪設的排污管道總長度最短.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,以O為原點,以x軸正半軸建立極坐標系,曲線C的極坐標方程為ρ2﹣4ρsinθ+3=0,直線l的參數方程為  ,(t為參數).
,(t為參數).
(1)寫出曲線C和直線l的直角坐標方程;
(2)若點A,B是曲線C上的兩動點,點P是直線l上一動點,求∠APB的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點列{An}、{Bn}分別在某銳角的兩邊上,且|AnAn+1|=|An+1An+2|,An≠An+1 , n∈N* , |BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+1 , n∈N* , (P≠Q表示點P與Q不重合)若dn=|AnBn|,Sn為△AnBnBn+1的面積,則( )
A.{Sn}是等差數列
B.{Sn2}是等差數列
C.{dn}是等差數列
D.{dn2}是等差數列
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知正三棱錐P﹣ABC的側面是直角三角形,PA=6,頂點P在平面ABC內的正投影為點D,D在平面PAB內的正投影為點E,連接PE并延長交AB于點G.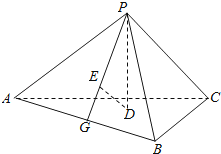
(1)證明:G是AB的中點;
(2)在圖中作出點E在平面PAC內的正投影F(說明作法及理由),并求四面體PDEF的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com