【題目】已知函數
.
（1）若
，求函數
的值域；
（2）討論函數的奇偶性，并說明理由.
【答案】（1）
； （2）當
時，函數
為偶函數；當
時，函數是奇函數；當
且
，函數既不是奇函數，也不是偶函數．.
【解析】
（1）將代入函數解析式，求得函數的定義域，將函數解析式化簡，之后借助于指數函數的值域以及不等式的性質求得結果；
（2）分類討論，利用奇偶函數的定義，討論函數的奇偶性，從而求得結果.
（1）當 時，定義域為
，
，
所以值域為
（2）①當時，
定義域為R，故函數
為偶函數；
②當且時，定義域為
不關于原點對稱，故函數既不是奇函數，也不是偶函數 ；
③當時，
定義域為
故函數是奇函數；
④當
時，定義域為R關于原點對稱，若是奇函數 
當
時，
故函數是奇函數；
若是偶函數
且
時，，函數既不是奇函數，也不是偶函數．
綜上：
當時，函數為偶函數；
當 
時，函數是奇函數；
當 且 
，函數既不是奇函數，也不是偶函數．
期末1卷素質教育評估卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
（b∈R）．若存在x∈[ 
，2]，使得f（x）+xf′（x）＞0，則實數 b的取值范圍是（ ）
A.（﹣∞， 
）
B.（﹣∞， 
）
C.（﹣∞，3）
D.（﹣∞， 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
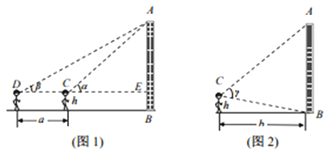
【題目】某校高一數學研究小組測量學校的一座教學樓AB的高度
已知測角儀器距離地面的高度為h米，現有兩種測量方法：
方法
如圖
用測角儀器，對準教學樓的頂部A，計算并記錄仰角
；
后退a米，重復
中的操作，計算并記錄仰角
．
方法
如圖
用測角儀器，對準教學樓的頂部A底部B，測出教學樓的視角
，測試點與教學樓的水平距離b米．
請你回答下列問題：
用數據
，
，a，h表示出教學樓AB的高度；
按照方法II，用數據
，b，h表示出教學樓AB的高度．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下面說法中錯誤的是（ ）
A. 經過定點
的直線都可以用方程
表示
B. 經過定點的直線都可以用方程
表示
C. 經過定點
的直線都可以用方程
表示
D. 不經過原點的直線都可以用方程
表示
E. 經過任意兩個不同的點
，
的直線都可以用方程
表示
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}為等差數列，a3=5，a7=13，數列{bn}的前n項和為Sn ， 且有Sn=2bn﹣1．
（1）求{an}、{bn}的通項公式；
（2）若cn=anbn ， {cn}的前n項和為Tn ， 求Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
，
為兩個不同的平面，
，
為兩條不同的直線，下列命題中正確的是（ ）
①若
，
，則
； ②若
，
，則
；
③若
，
，
，則
④若
，
，
，則.
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓心為
的圓，滿足下列條件：圓心位于
軸正半軸上，與直線
相切，且被
軸截得的弦長為
，圓的面積小于13.
（1）求圓的標準方程；
（2）若點
，點
是圓上一點，點
是
的重心，求點的軌跡方程；
（3）設過點
的直線
與圓交于不同的兩點
，
，以
，
為鄰邊作平行四邊形
.是否存在這樣的直線，使得直線
與
恰好平行？如果存在，求出的方程；如果不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】分形幾何學是美籍法國數學家伯努瓦
曼德爾布羅特（
）在20世紀70年代創立的一門新學科，它的創立為解決傳統眾多領域的難題提供了全新的思路.下圖是按照分型的規律生長成的一個樹形圖，則第10行的空心圓的個數是__________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
