【題目】已知銳角△ABC中，內角
所對應的邊分別為
，且滿足：
，
，則
的取值范圍是____________．
【答案】
【解析】分析：由已知可得：b2=2a+a2，又由余弦定理可得：b2=a2+4-4acosB，整理可得：
，可求B的范圍，進而可求cosB的范圍，進而可求a的范圍．
詳解：：∵b2-a2=ac，c=2，可得：b2=2a+a2，又∵由余弦定理可得：b2=a2+c2-2accosB=a2+4-4acosB，
∴2a+a2=a2+4-4acosB，整理可得：，∵由余弦定理2bccosA=b2+c2-a2=c2+ac，可得：2bcosA=c+a，
∴由正弦定理可得：2sinBcosA=sinC+sinA=sin（A+B）+sinA=sinAcosB+cosAsinB+sinA，
可得：sinBcosA-sinAcosB=sinA，可得：sin（B-A）=sinA，可得：B-A=A，或B-A=π-A（舍去），可得：B=2A，C=π-A-B=π-3A，由△ABC為銳角三角形，可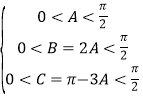得：
解得：
可得：cosB∈
,∴可得：1+2cosB∈（1，2），∈（1，2），故答案為：（1，2）．
科目：高中數學 來源： 題型：
【題目】過 
軸上動點 
引拋物線 
的兩條切線 
、 
， 
、 
為切點，設切線 、 的斜率分別為 
和 
.
（Ⅰ）求證： 
；
（Ⅱ）求證：直線 
恒過定點，并求出此定點坐標；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】長方體
中，O是坐標原點，OA是
軸，OC是
軸，
是
軸．E是AB中點，F是
中點，OA=3，OC=4，
=3，則F坐標為（ ）
A. （3，2，
） B. （3，3，）
C. （3，，2） D. （3，0，3）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC的角A，B，C所對的邊分別為a，b，c，設向量
＝(a，b)，
＝(sin B，sin A)， 
＝(b－2，a－2)．
(1)若∥，求證：△ABC為等腰三角形；
(2)若⊥，邊長c＝2，∠C＝
，求△ABC的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
