
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,過
,過![]() 作互相垂直的兩條直線分別與
作互相垂直的兩條直線分別與![]() 相交于
相交于![]() ,
,![]() 和
和![]() ,
,![]() 四點.
四點.
(1)四邊形![]() 能否成為平行四邊形,請說明理由;
能否成為平行四邊形,請說明理由;
(2)求![]() 的最小值.
的最小值.
【答案】(1)見解析.
(2)![]() .
.
【解析】
試題分析:(1)若四邊形![]() 為平行四邊形,則四邊形
為平行四邊形,則四邊形![]() 為菱形, ∴
為菱形, ∴![]() 與
與![]() 在點
在點![]() 處互相平分,又
處互相平分,又![]() 的坐標為
的坐標為![]() 顯然這時
顯然這時![]() 不是平行四邊形.
不是平行四邊形.
(2)直線![]() 的斜率存在且不為零時,設直線
的斜率存在且不為零時,設直線![]() 的方程為
的方程為![]() ,與橢圓方程聯立,消去
,與橢圓方程聯立,消去![]() ,利用韋達定理及弦長公式
,利用韋達定理及弦長公式![]() ,
,
令![]() ,則
,則![]() .考慮當直線
.考慮當直線![]() 的斜率不存在時和直線
的斜率不存在時和直線![]() 的斜率為零時情況得到
的斜率為零時情況得到![]() 的最小值
的最小值
試題解析:設點![]()
(Ⅰ)若四邊形![]() 為平行四邊形,則四邊形
為平行四邊形,則四邊形![]() 為菱形,
為菱形,
∴![]() 與
與![]() 在點
在點![]() 處互相平分,又F的坐標為
處互相平分,又F的坐標為![]() ,由橢圓的對稱性知
,由橢圓的對稱性知![]() 垂直于
垂直于![]() 軸,則
軸,則![]() 垂直于
垂直于![]() 軸,
軸,
顯然這時![]() 不是平行四邊形.
不是平行四邊形.
∴四邊形![]() 不可能成為平行四邊形.
不可能成為平行四邊形.
(Ⅱ) 當直線![]() 的斜率存在且不為零時,設直線
的斜率存在且不為零時,設直線![]() 的方程為
的方程為![]()
由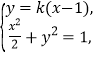 消去
消去![]() 得,
得,![]()
∴![]()
∴![]() 同理得,
同理得,![]() .∴
.∴![]() ,
,
令![]() ,則
,則![]() .
.
當直線![]() 的斜率不存在時,則
的斜率不存在時,則![]()
當直線![]() 的斜率為零時,則
的斜率為零時,則![]()
![]() ,∴
,∴![]() 的最小值為
的最小值為![]() .
.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數學 來源: 題型:
【題目】已知圓![]() 經過兩點
經過兩點![]() ,
,![]() ,且圓心
,且圓心![]() 在直線
在直線![]() :
:![]() 上.
上.
(1)求圓![]() 的方程;
的方程;
(2)設圓![]() 與
與![]() 軸相交于
軸相交于![]() 、
、![]() 兩點,點
兩點,點![]() 為圓
為圓![]() 上不同于
上不同于![]() 、
、![]() 的任意一點,直線
的任意一點,直線![]() 、
、![]() 交
交![]() 軸于
軸于![]() 、
、![]() 點.當點
點.當點![]() 變化時,以
變化時,以![]() 為直徑的圓
為直徑的圓![]() 是否經過圓
是否經過圓![]() 內一定點?請證明你的結論.
內一定點?請證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某屆世界杯足球賽上,a,b,c,d四支球隊進入了最后的比賽,在第一輪的兩場比賽中,a對b,c對d,然后這兩場比賽的勝者將進入冠亞軍決賽,這兩場比賽的負者比賽,決出第三名和第四名.比賽的一種最終可能結果記為acbd(表示a勝b,c勝d,然后a勝c,b勝d).
(1)寫出比賽所有可能結果構成的樣本空間;
(2)設事件A表示a隊獲得冠軍,寫出A包含的所有可能結果;
(3)設事件B表示a隊進入冠亞軍決賽,寫出B包含的所有可能結果.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于圓周率![]() ,數學發展史上出現過許多很有創意的求法,如著名的蒲豐試驗.受其啟發,我們也可以通過設計下面的試驗來估計
,數學發展史上出現過許多很有創意的求法,如著名的蒲豐試驗.受其啟發,我們也可以通過設計下面的試驗來估計![]() 的值,試驗步驟如下:①先請高二年級 500名同學每人在小卡片上隨機寫下一個實數對
的值,試驗步驟如下:①先請高二年級 500名同學每人在小卡片上隨機寫下一個實數對![]() ;②若卡片上的
;②若卡片上的![]() 能與1構成銳角三角形,則將此卡片上交;③統計上交的卡片數,記為
能與1構成銳角三角形,則將此卡片上交;③統計上交的卡片數,記為![]() ;④根據統計數
;④根據統計數![]() 估計
估計![]() 的值.假如本次試驗的統計結果是
的值.假如本次試驗的統計結果是![]() ,那么可以估計
,那么可以估計![]() 的值約為( )
的值約為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義域為![]() 的函數
的函數![]() 滿足:對于任意的實數
滿足:對于任意的實數![]() 都有
都有![]() 成立,且當
成立,且當![]() 時,
時, ![]() 恒成立,且
恒成立,且![]() 是一個給定的正整數).
是一個給定的正整數).
(1)判斷函數![]() 的奇偶性,并證明你的結論;
的奇偶性,并證明你的結論;
(2)判斷并證明![]() 的單調性;若函數
的單調性;若函數![]() 在
在![]() 上總有
上總有![]() 成立,試確定
成立,試確定![]() 應滿足的條件;
應滿足的條件;
(3)當![]() 時,解關于
時,解關于![]() 的不等式
的不等式![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設有5個條件類似的女孩(把她們分別記為A,B,C,D, E)應聘秘書工作,但只有2個秘書職位,因此5個人中只有2人能被錄用.如果5個人被錄用的機會相等,分別計算下列事件的概率;
(1)女孩A得到一個職位;
(2)女孩A和B各得到一個職位;
(3)女孩A或B得到一個職位.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,點P,G分別是
中,點P,G分別是![]() ,
,![]() 的中點,已知
的中點,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求異面直線![]() 與AB所成角的余弦值;
與AB所成角的余弦值;
(II)求證:![]() ⊥平面
⊥平面![]() ;
;
(III)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知離心率為![]() 的橢圓C:
的橢圓C:![]() (a>b>0)的左焦點為
(a>b>0)的左焦點為![]() ,過
,過![]() 作長軸的垂線交橢圓于
作長軸的垂線交橢圓于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(I)求橢圓C的標準方程;
(II)設O為原點,若點A在直線![]() 上,點B在橢圓C上,且
上,點B在橢圓C上,且![]() ,求線段AB長度的最小值.
,求線段AB長度的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com