【題目】假設(shè)有5個條件類似的女孩（把她們分別記為A，B，C，D， E）應(yīng)聘秘書工作，但只有2個秘書職位，因此5個人中只有2人能被錄用.如果5個人被錄用的機會相等，分別計算下列事件的概率；
（1）女孩A得到一個職位；
（2）女孩A和B各得到一個職位；
（3）女孩A或B得到一個職位.
科目：高中數(shù)學(xué) 來源： 題型：
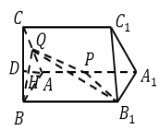
【題目】如圖，三棱柱
中，四邊形
為菱形，
，平面
平面
，
在線段
上移動，
為棱
的中點.
（1）若為線段的中點，
為
中點，延長
交
于
，求證：
平面
；
（2）若二面角
的平面角的余弦值為
，求點到平面
的距離.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示的莖葉圖記錄了華潤萬家在渭南城區(qū)甲、乙連鎖店四天內(nèi)銷售情況的某項指標(biāo)統(tǒng)計：
（I）求甲、乙連鎖店這項指標(biāo)的方差，并比較甲、乙該項指標(biāo)的穩(wěn)定性；
（Ⅱ）每次都從甲、乙兩店統(tǒng)計數(shù)據(jù)中隨機各選一個進(jìn)行比對分析，共選了3次（有放回選取）．設(shè)選取的兩個數(shù)據(jù)中甲的數(shù)據(jù)大于乙的數(shù)據(jù)的次數(shù)為
，求的分布列及數(shù)學(xué)期望
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
：
的右焦點為
，過作互相垂直的兩條直線分別與相交于
，
和
，
四點.
（1）四邊形
能否成為平行四邊形，請說明理由；
（2）求
的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】一個盒子中裝有標(biāo)號為1,2,3,4,5的5張標(biāo)簽，隨機地依次選取兩張標(biāo)簽，根據(jù)下列條件求兩張標(biāo)簽上的數(shù)字為相等整數(shù)的概率；
（1）標(biāo)簽的選取是不放回的；
（2）標(biāo)簽的選取是有放回的.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某心理學(xué)研究小組在對學(xué)生上課注意力集中情況的調(diào)查研究中，發(fā)現(xiàn)其注意力指數(shù)p與聽課時間t之間的關(guān)系滿足如圖所示的曲線．當(dāng)t∈(0,14]時，曲線是二次函數(shù)圖象的一部分，當(dāng)t∈[14,40]時，曲線是函數(shù)
（
且
）圖象的一部分．根據(jù)專家研究，當(dāng)注意力指數(shù)p大于等于80時聽課效果最佳．
(1)試求
的函數(shù)關(guān)系式；
(2)一道數(shù)學(xué)難題，講解需要22分鐘，問老師能否經(jīng)過合理安排在學(xué)生聽課效果最佳時講完？請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某工廠生產(chǎn)某種型號的電視機零配件，為了預(yù)測今年
月份該型號電視機零配件的市場需求量，以合理安排生產(chǎn)，工廠對本年度
月份至
月份該型號電視機零配件的銷售量及銷售單價進(jìn)行了調(diào)查，銷售單價
（單位：元）和銷售量
（單位：千件）之間的組數(shù)據(jù)如下表所示：
月份 |
|
|
|
|
|
|
銷售單價 |
|
|
|
|
|
|
銷售量 |
|
|
|
|
|
|
（1）根據(jù)1至月份的數(shù)據(jù)，求關(guān)于的線性回歸方程（系數(shù)精確到
）；
（2）結(jié)合（1）中的線性回歸方程，假設(shè)該型號電視機零配件的生產(chǎn)成本為每件
元，那么工廠如何制定月份的銷售單價，才能使該月利潤達(dá)到最大（計算結(jié)果精確到
）？
參考公式：回歸直線方程
，其中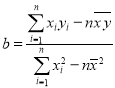
.
參考數(shù)據(jù)：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某品牌計算機售后保修期為1年，根據(jù)大量的維修記錄資料，這種品牌的計算機在使用一年內(nèi)需要維修1次的占15%，需要維修2次的占6%，需要維修3次的占4%.
（1）某人購買了一臺這個品牌的計算機，設(shè)
=“一年內(nèi)需要維修k次”，k=0,1,2,3,請?zhí)顚懴卤恚?/span>
事件 |
|
|
|
|
概率 |
事件
是否滿足兩兩互斥？是否滿足等可能性？
（2）求下列事件的概率：
①A=“在1年內(nèi)需要維修”;
②B=“在1年內(nèi)不需要維修”；
③C=“在1年內(nèi)維修不超過1次”.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知平面內(nèi)點
到點
的距離和到直線
的距離之比為
，若動點P的軌跡為曲線C．
（I）求曲線C的方程；
（II）過F的直線
與C交于A，B兩點，點M的坐標(biāo)為
設(shè)O為坐標(biāo)原點.證明：
．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
