
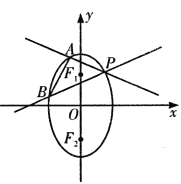
【題目】已知橢圓![]() 兩焦點分別為
兩焦點分別為![]() 是橢圓在第一象限弧上一點,并滿足
是橢圓在第一象限弧上一點,并滿足![]() ,過P作傾斜角互補的兩條直線
,過P作傾斜角互補的兩條直線![]() 分別交橢圓于
分別交橢圓于![]() 兩點.
兩點.
(1)求![]() 點坐標;
點坐標;
(2)求證:直線![]() 的斜率為定值;
的斜率為定值;
(3)求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() ; (2)證明見解析;(3)
; (2)證明見解析;(3) ![]() .
.
【解析】
(1)設出![]() 的坐標,則可分別表示出
的坐標,則可分別表示出![]() 和
和![]() ,進而利用
,進而利用![]() 求得
求得![]() 和
和![]() 的關系,同時根據
的關系,同時根據![]() 求得
求得![]() 和
和![]() 即
即![]() 的坐標;(2)設出
的坐標;(2)設出![]() 的方程,與橢圓方程聯立根據
的方程,與橢圓方程聯立根據![]() ,表示出
,表示出![]() 和
和![]() ,同理表示出點
,同理表示出點![]() 的坐標,進而求得
的坐標,進而求得![]() 的斜率,化簡即可得結果;(3)設出
的斜率,化簡即可得結果;(3)設出![]() 的方程與橢圓的方程聯立,利用韋達定理表示出
的方程與橢圓的方程聯立,利用韋達定理表示出![]() 和
和![]() ,進而求得
,進而求得![]() ,最后利用弦長公式求得
,最后利用弦長公式求得![]() 的長,利用三角形面積公式表示出三角形面積,結合基本不等式即可得到結論.
的長,利用三角形面積公式表示出三角形面積,結合基本不等式即可得到結論.
(1)由題可得![]() ,
,
設![]() ,
,
則![]() ,
,
![]() ,
,
![]() 點
點![]() 在曲線上,則
在曲線上,則![]() ,
,
從而![]() ,得
,得![]() ,
,
則點![]() 的坐標為
的坐標為![]() .
.
(2)由題意知,兩直線![]() 的斜率必存在,設
的斜率必存在,設![]() 的斜率為
的斜率為![]() ,
,
則![]() 的直線方程為
的直線方程為![]() ,
,
由 得
得![]() ,
,
設![]() ,則
,則![]() ,
,
同理可得![]() ,
,
則![]() ,
,
![]() 的斜率
的斜率![]() 為定值.
為定值.
(3)設![]() 的直線方程
的直線方程![]() ,
,
 得
得![]() ,
,
由![]() 得
得![]() ,
,
![]() 到
到![]() 的距離為
的距離為![]() ,
,
則![]()
 ,
,
當且僅當![]() 時取等號,
時取等號,
![]() 三角形
三角形![]() 面積的最大值為
面積的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】現在,很多人都喜歡騎“共享單車”,但也有很多市民并不認可.為了調查人們對這種交通方式的認可度,某同學從交通擁堵不嚴重的A城市和交通擁堵嚴重的B城市分別隨機調查了20名市民,得到了一個市民是否認可的樣本,具體數據如下![]() 列聯表:
列聯表:
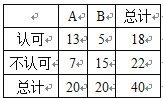
附:![]() ,
,![]() .
.

根據表中的數據,下列說法中,正確的是( )
A. 沒有95% 以上的把握認為“是否認可與城市的擁堵情況有關”
B. 有99% 以上的把握認為“是否認可與城市的擁堵情況有關”
C. 可以在犯錯誤的概率不超過0.01的前提下認為“是否認可與城市的擁堵情況有關”
D. 可以在犯錯誤的概率不超過0.025的前提下認為“是否認可與城市的擁堵情況有關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年郴州市兩會召開前夕,某網站推出兩會熱點大型調查,調查數據表明,民生問題時百姓最為關心的熱點,參與調查者中關注此問題的約占80%,現從參與者中隨機選出200人,并將這200人按年齡分組:第1組[15,25),第2組[25,35),第3組[35,45),第4組[45,55),第5組[55,65),得到的頻率分布直方圖如圖所示. 
(1)求出頻率分布直方圖中的a值,并求出這200的平均年齡;
(2)現在要從年齡較小的第1,2,3組用分層抽樣的方法抽取12人,再從這12人中隨機抽取3人贈送禮品,求抽取的3人中至少有1人的年齡在第3組的概率;
(3)若要從所有參與調查的人(人數很多)中隨機選出3人,記關注民生問題的人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,曲線C的參數方程為 ![]() (θ為參數),直線l的參數方程為
(θ為參數),直線l的參數方程為  (t為參數)以坐標原點O為極點,x軸的正半軸為極軸的極坐標系.
(t為參數)以坐標原點O為極點,x軸的正半軸為極軸的極坐標系.
(1)寫出直線l的普通方程以及曲線C的極坐標方程;
(2)若直線l與曲線C的兩個交點分別為M,N,直線l與x軸的交點為P,求|PM||PN|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐P﹣ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分別為PB,BC的中點.
(1)求證:DE∥平面PAC;
(2)求證:DE⊥AD.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大提出,堅決打贏脫貧攻堅戰,某幫扶單位為幫助定點扶貧村真脫貧,堅持扶貧同扶智相結合,幫助貧困村種植蜜柚,并利用電商進行銷售,為了更好地銷售,現從該村的蜜柚樹上隨機摘下了100個蜜柚進行測重,其質量分別在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (單位:克)中,其頻率分布直方圖如圖所示.
(單位:克)中,其頻率分布直方圖如圖所示.

(1)求質量落在![]() ,
, ![]() 兩組內的蜜柚的抽取個數,
兩組內的蜜柚的抽取個數,
(2)從質量落在![]() ,
, ![]() 內的蜜柚中隨機抽取2個,求這2個蜜柚質量均小于2000克的概率;
內的蜜柚中隨機抽取2個,求這2個蜜柚質量均小于2000克的概率;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設p:實數x滿足x2﹣4ax+3a2<0,q:實數x滿足|x﹣3|<1.
(1)若a=1,且p∧q為真,求實數x的取值范圍;
(2)若其中a>0且¬p是¬q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com