
【題目】如圖1是四棱錐的直觀圖,其正(主)視圖和側(左)視圖均為直角三角形,俯視圖外框為矩形,相關數據如圖2所示.
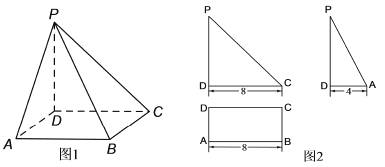
(1)設![]() 中點為
中點為![]() ,在直線
,在直線![]() 上找一點
上找一點![]() ,使得
,使得![]() 平面
平面![]() ,并說明理由;
,并說明理由;
(2)若二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() ,求四棱錐
,求四棱錐![]() 的外接球的表面積.
的外接球的表面積.
【答案】(1) 見解析;(2) ![]() .
.
【解析】試題分析:(1)利用中位線定理構造平行四邊形,得到![]() ;(2) 由二面角
;(2) 由二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() ,得到
,得到![]() ,明確外接球的直徑即為PB,易得四棱錐
,明確外接球的直徑即為PB,易得四棱錐![]() 的外接球的表面積.
的外接球的表面積.
試題解析:
(1)當![]() 是
是![]() 中點時,
中點時, ![]() 平面
平面![]() ,
,
證明如下:取![]() 中點
中點![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,
,
在![]() 中,
中, ![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,
∴![]() 是
是![]() 的中位線,
的中位線,
∴![]() 且
且![]() ,又
,又![]() 是
是![]() 中點,
中點, ![]() ,
,
∴![]() 且
且![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() .
.
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
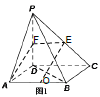
(2)由三視圖可得![]() 平面
平面![]() ,
,
在底面![]() 中,過
中,過![]() 作
作![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,
的平面角,
在底面矩形![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
在![]() 中,又
中,又![]() ,
,
∴![]() ,∴
,∴![]() .
.
由直觀圖易知四棱錐![]() 的外接球的直徑即為
的外接球的直徑即為![]() ,
,
∴![]() .
.
故四棱錐![]() 的外接球的表面積為
的外接球的表面積為![]() .
.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:高中數學 來源: 題型:
【題目】現有6名奧運會志愿者,其中志愿者![]() 通曉日語,
通曉日語, ![]() 通曉俄語,
通曉俄語, ![]() 通曉韓語,從中選出通曉日語、俄語和韓語的志愿者各1名,組成一個小組.
通曉韓語,從中選出通曉日語、俄語和韓語的志愿者各1名,組成一個小組.
(1)求![]() 被選中的概率;
被選中的概率;
(2)求![]() 和
和![]() 不全被選中的概率;
不全被選中的概率;
(3)若6名奧運會志愿者每小時派兩人值班,現有兩名只會日語的運動員到來,求恰好遇到![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.如圖,網格紙上正方形小格的邊長為1,圖中粗線畫出的是某幾何體毛坯的三視圖,第一次切削,將該毛坯得到一個表面積最大的長方體;第二次切削沿長方體的對角面刨開,得到兩個三棱柱;第三次切削將兩個三棱柱分別沿棱和表面的對角線刨開得到兩個鱉臑和兩個陽馬,則陽馬與鱉臑的體積之比為( )
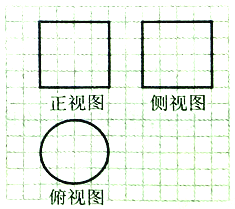
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數,
為常數,![]() 是自然對數的底數),曲線
是自然對數的底數),曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸平行.
軸平行.
(1)求![]() 的值;
的值;
(2)求![]() 的單調區間;
的單調區間;
(3)設![]() ,其中
,其中![]() 為
為![]() 的導函數.證明:對任意
的導函數.證明:對任意![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,矩形ABCD的一邊AB在x軸上,另一邊CD在x軸上方,且AB=8,BC=6,其中A(-4,0)、B(4,0)
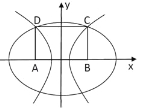
(1)若A、B為橢圓的焦點,且橢圓經過C、D兩點,求該橢圓的方程;
(2)若A、B為雙曲線的焦點,且雙曲線經過C、D兩點,求雙曲線的方程;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設不等式組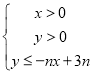 所表示的平面區域為Dn,記Dn內的格點(格點即橫坐標和縱坐標均為整數的點)的個數為f(n)(n∈N*).
所表示的平面區域為Dn,記Dn內的格點(格點即橫坐標和縱坐標均為整數的點)的個數為f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表達式;
(2)設bn=2nf(n),Sn為{bn}的前n項和,求Sn;
(3)記![]() ,若對于一切正整數n,總有Tn≤m成立,求實數m的取值范圍.
,若對于一切正整數n,總有Tn≤m成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
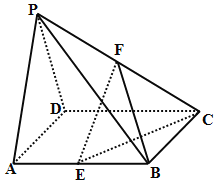
【題目】如圖所示,在四棱錐P-ABCD中,底面ABCD是棱長為2的正方形,側面PAD為正三角形,且面PAD⊥面ABCD,E、F分別為棱AB、PC的中點.
(1)求證:EF∥平面PAD;
(2)求三棱錐B-EFC的體積;
(3)求二面角P-EC-D的正切值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com