
【題目】(1)求經過點![]() ,且離心率為
,且離心率為![]() 的橢圓的標準方程;
的橢圓的標準方程;
(2)已知雙曲線![]() 與橢圓
與橢圓![]() :
:![]() 有相同的焦點,且過點
有相同的焦點,且過點![]() ,求雙曲線
,求雙曲線![]() 的標準方程.
的標準方程.
【答案】(1)![]() 或
或![]() .(2)
.(2)![]()
【解析】
(1)討論焦點在在x軸上或焦點在y軸上.根據離心率、端點坐標,結合橢圓中![]() ,可求得橢圓的標準方程.
,可求得橢圓的標準方程.
(2)根據橢圓的標準方程,可求得焦點坐標.代入點的坐標,結合![]() ,即可求得雙曲線的標準方程.
,即可求得雙曲線的標準方程.
(1)若橢圓的焦點在x軸上,設其方程為![]() (
(![]() ),
),
因為經過點![]() ,且離心率為
,且離心率為![]() ,所以
,所以![]() ,
,![]() ,
,
又![]() ,得
,得![]() ,
,
所以橢圓的標準方程為![]() .
.
若橢圓的焦點在y軸上,設其方程為![]() (
(![]() ),
),
因為經過點![]() ,且離心率為
,且離心率為![]() ,所以
,所以![]() ,
,![]() ,又
,又![]() ,得
,得![]() ,
,
所以橢圓的標準方程為![]() .
.
綜上,橢圓的標準方程為![]() 或
或![]() .
.
(2)因為橢圓![]() 的焦點為
的焦點為![]() ,
,![]() ,且雙曲線與橢圓有相同的焦點,
,且雙曲線與橢圓有相同的焦點,
所以設雙曲線的標準方程為![]() (
(![]() ,
,![]() ),
),
得![]() ,又雙曲線過點
,又雙曲線過點![]() ,得
,得![]() ,
,
聯立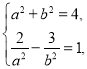 解得
解得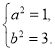
所以雙曲線的標準方程為![]() .
.


 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案 激活思維優加課堂系列答案
激活思維優加課堂系列答案科目:高中數學 來源: 題型:
【題目】在梯形![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,線段
的中點,線段![]() 與
與![]() 交于
交于![]() 點(如圖1).將
點(如圖1).將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 為直二面角(如圖2).
為直二面角(如圖2).
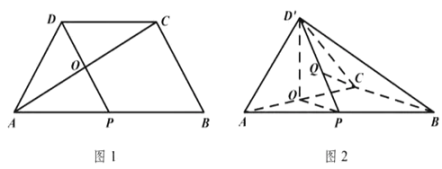
(1)求證:![]() 平面
平面![]() ;
;
(2)線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某工廠生產的某種產品中抽取1000件,測量這些產品的一項質量指標值,由測量結果得如下頻率分布直方圖:
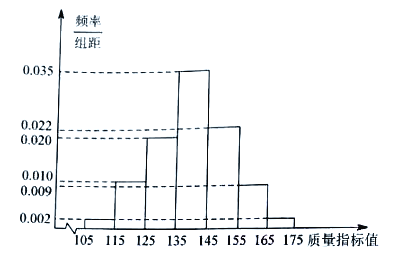
(1)求這1000件產品質量指標值的樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組數據用該區間的中點值作代表)
(同一組數據用該區間的中點值作代表)
(2)由頻率分布直方圖可以認為,這種產品的質量指標值![]() 服從正態分布
服從正態分布![]() ,其中以
,其中以![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
(ⅰ)利用該正態分布,求![]() ;
;
(ⅱ)某用戶從該工廠購買了100件這種產品,記![]() 表示這100件產品中質量指標值為于區間(127.6,140)的產品件數,利用(ⅰ)的結果,求
表示這100件產品中質量指標值為于區間(127.6,140)的產品件數,利用(ⅰ)的結果,求![]() .
.
附:![]() .若
.若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大城市往往人口密集,城市綠化在健康人民群眾肺方面發揮著非常重要的作用,歷史留給我們城市里的大山擁有品種繁多的綠色植物更是無價之寶.改革開放以來,有的地方領導片面追求政績,對森林資源野蠻開發受到嚴肅查處事件時有發生.2019年的春節后,廣西某市林業管理部門在“綠水青山就是金山銀山”理論的不斷指引下,積極從外地引進甲、乙兩種樹苗,并對甲、乙兩種樹苗各抽測了10株樹苗的高度(單位:厘米),數據如下面的莖葉圖:
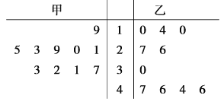
(1)據莖葉圖求甲、乙兩種樹苗的平均高度;
(2)據莖葉圖,運用統計學知識分析比較甲、乙兩種樹苗高度整齊情況.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型工廠有![]() 臺大型機器,在
臺大型機器,在![]() 個月中,
個月中,![]() 臺機器至多出現
臺機器至多出現![]() 次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需
次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需![]() 名工人進行維修.每臺機器出現故障的概率為
名工人進行維修.每臺機器出現故障的概率為![]() .已知
.已知![]() 名工人每月只有維修
名工人每月只有維修![]() 臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得
臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得![]() 萬元的利潤,否則將虧損
萬元的利潤,否則將虧損![]() 萬元.該工廠每月需支付給每名維修工人
萬元.該工廠每月需支付給每名維修工人![]() 萬元的工資.
萬元的工資.
(1)若每臺機器在當月不出現故障或出現故障時有工人進行維修,則稱工廠能正常運行.若該廠只有![]() 名維修工人,求工廠每月能正常運行的概率;
名維修工人,求工廠每月能正常運行的概率;
(2)已知該廠現有![]() 名維修工人.
名維修工人.
(ⅰ)記該廠每月獲利為![]() 萬元,求
萬元,求![]() 的分布列與數學期望;
的分布列與數學期望;
(ⅱ)以工廠每月獲利的數學期望為決策依據,試問該廠是否應再招聘![]() 名維修工人?
名維修工人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為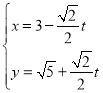 (
(![]() 為參數)。在極坐標系(與直角坐標系
為參數)。在極坐標系(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的極坐標方程為
的極坐標方程為![]() 。
。
(1)求直線![]() 的普通方程和圓
的普通方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設圓![]() 與直線
與直線![]() 交于
交于![]() ,
,![]() 兩點,若點
兩點,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左焦點為
的左焦點為![]() ,上頂點為
,上頂點為![]() .已知橢圓的短軸長為4,離心率為
.已知橢圓的短軸長為4,離心率為![]() .
.
(1)求橢圓的方程;
(2)設點![]() 在橢圓上,且異于橢圓的上、下頂點,點
在橢圓上,且異于橢圓的上、下頂點,點![]() 為直線
為直線![]() 與
與![]() 軸的交點,點
軸的交點,點![]() 在
在![]() 軸的負半軸上.若
軸的負半軸上.若![]() (
(![]() 為原點),且
為原點),且![]() ,求證:直線
,求證:直線![]() 的斜率與直線MN的斜率之積為定值.
的斜率與直線MN的斜率之積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在數列{an}中,設a1為首項,其前n項和為Sn,若對任意的正整數m,n都有不等式S2m+S2n<2Sm+n(m≠n)恒成立,且2S6<S3.
(1)設數列{an}為等差數列,且公差為d,求![]() 的取值范圍;
的取值范圍;
(2)設數列{an}為等比數列,且公比為q(q>0且q≠1),求a1![]() q的取值范圍.
q的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com