【題目】已知函數
.
(1)求函數
的單調區間;
(2)當
時,函數
的圖象恒不在
軸的上方,求實數
的取值范圍.
【答案】（1）見解析；（2）
【解析】試題分析：(1)對函數求導，對參數
分類討論,利用導數的正負求得函數的單調區間；(2)將問題轉化為
，由
得
，令
，則
，對參數
分類討論，分別求得函數
的最大值，利用函數
的最大值不小于零,求得參數
的取值范圍.
試題解析：(1) 
的定義域為
①當
時,則
,所以
在
上單調遞增;
②當
時,則由
知
,由
知
,
所以
在
上單調遞增,在
上單調遞減;
綜上,當
時, 
的單調遞增區間為
,
當
時, 
的單調遞增區間為
,單調遞減區間為
.
(2)由題意知: 
恒成立,
而
0
0
,
由
,得: 
.
令
,則
,
①若
在
上單調遞增，故
,
在
上單調遞增, 
，
從而
,不符合題意；
②若
，當
時, 
在
上單調遞增,
從而
,
所以
在
上單調遞增, 
,
從而在
上
,不符合題意;
③若
在
上恒成立,
在
上單調遞減, 
,
從而
在
上單調遞減, 
,
所以
恒成立，綜上所述, 
的取值范圍是
科目：高中數學 來源： 題型：
【題目】已知向量
， 
，函數
，函數
在
軸上的截距我
，與
軸最近的最高點的坐標是
．
（Ⅰ）求函數
的解析式；
（Ⅱ）將函數
的圖象向左平移
（
）個單位，再將圖象上各點的縱坐標不變，橫坐標伸長到原來的2倍，得到函數
的圖象，求
的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設某校新、老校區之間開車單程所需時間為
，只與道路暢通狀況有關，對其容量為
的樣本進行統計，結果如圖：
| 25 | 30 | 35 | 40 |
頻數（次） | 20 | 30 | 40 | 10 |
（1）求的分布列與數學期望
；
（2）劉教授駕車從老校區出發，前往新校區做一個50分鐘的講座，結束后立即返回老校區，求劉教授從離開老校區到返回老校區共用時間不超過120分鐘的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校組織學生參加英語測試，成績的頻率分布直方圖如圖，數據的分組一次為[20，40），[40，60），[60，80），[80，100）．若低于60分的人數是15人，則該班的學生人數是（ ）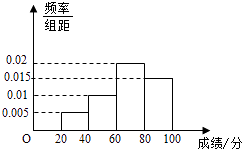 
A.45
B.50
C.55
D.60
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
