
【題目】已知圓![]() ,直線
,直線![]() 被圓所截得的弦的中點為
被圓所截得的弦的中點為![]() .
.
(1)求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相交, 求
相交, 求![]() 的取值范圍;
的取值范圍;
(3)是否存在常數![]() ,使得直線
,使得直線![]() 被圓
被圓![]() 所截得的弦中點落在直線
所截得的弦中點落在直線![]() 上?若存在, 求出
上?若存在, 求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)設直線![]() 的斜率為則
的斜率為則![]() ,由題意可得圓心
,由題意可得圓心![]() ,又弦的中點為
,又弦的中點為![]() ,可求得
,可求得![]() ,由
,由![]() 可求
可求![]() ,從而可求直線
,從而可求直線![]() 的方程;(2)若直線
的方程;(2)若直線![]() :
:![]() 與圓
與圓![]() 相交,圓心到直線
相交,圓心到直線![]() 的距離小于半徑,從而可求得
的距離小于半徑,從而可求得![]() 的取值范圍;(3)設直線
的取值范圍;(3)設直線![]() 被圓
被圓![]() 解得的弦的中點為
解得的弦的中點為![]() ,由直線
,由直線![]() 與
與![]() 垂直,可得
垂直,可得![]() ,與
,與![]() 聯立可求得
聯立可求得![]() ,代入直線
,代入直線![]() 的方程,求得
的方程,求得![]() ,驗證即可.
,驗證即可.
試題解析:(1)圓![]() 方程化為標準方程:
方程化為標準方程:![]() ,則其圓心
,則其圓心![]() ,半徑
,半徑![]() ,若設直線
,若設直線![]() 的斜率為
的斜率為![]() ,則
,則 ,
,![]() 直線
直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
(2)![]() 圓的半徑
圓的半徑![]() ,
,![]() 要直線
要直線![]() 與圓
與圓![]() 相交, 則須有
相交, 則須有![]() ,于是
,于是![]() 的取值范圍是
的取值范圍是![]() .
.
(3)設直線![]() 被圓
被圓![]() 截得的弦的中點為
截得的弦的中點為![]() ,則直線
,則直線![]() 與
與![]() 垂直, 于是有
垂直, 于是有![]() ,整理可得
,整理可得![]() ,又
,又![]() 點
點![]() 在直線
在直線![]() 上,
上, ![]() ,
,![]() 由
由 ,解得
,解得 ,代入直線
,代入直線![]() 的方程, 得
的方程, 得![]() ,于是
,于是![]() ,故存在滿足條件的常數
,故存在滿足條件的常數![]() .
.


科目:高中數學 來源: 題型:
【題目】已知某中學聯盟舉行了一次“盟校質量調研考試”活動.為了解本次考試學生的某學科成績情況,從中抽取部分學生的分數(滿分為100分,得分取正整數,抽取學生的分數均在![]() 之內)作為樣本(樣本容量為n)進行統計.按照
之內)作為樣本(樣本容量為n)進行統計.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() 的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(莖葉圖中僅列出了得分在
的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(莖葉圖中僅列出了得分在![]() ,
,![]() 的數據).
的數據).
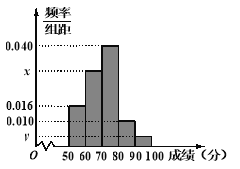
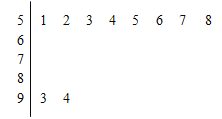
(Ⅰ)求樣本容量n和頻率分布直方圖中的x、y的值;
(Ⅱ)在選取的樣本中,從成績在80分以上(含80分)的學生中隨機抽取2名學生參加“省級學科基礎知識競賽”,求所抽取的2名學生中恰有一人得分在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某小區準備將一塊閑置的直角三角形(其中![]() )土地開發成公共綠地,設計時,要求綠地部分(圖中陰影部分)有公共綠地走道
)土地開發成公共綠地,設計時,要求綠地部分(圖中陰影部分)有公共綠地走道![]() ,且兩邊是兩個關于走道
,且兩邊是兩個關于走道![]() 對稱的三角形(
對稱的三角形(![]() 和
和![]() ),現考慮方便和綠地最大化原則,要求
),現考慮方便和綠地最大化原則,要求![]() 點與
點與![]() 點不重合,
點不重合,![]() 點落在邊
點落在邊![]() 上,設
上,設![]() .
.
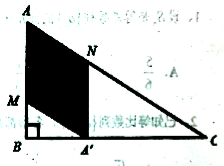
(1)若![]() ,綠地“最美”,求最美綠地的面積;
,綠地“最美”,求最美綠地的面積;
(2)為方便小區居民行走,設計時要求![]() 最短,求此時公共綠地走道
最短,求此時公共綠地走道![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中日“釣魚島爭端”問題越來越引起社會關注,我校對高一![]() 名學生進行了一次“釣魚島”知識測試,并從中抽取了部分學生的成績,(滿分
名學生進行了一次“釣魚島”知識測試,并從中抽取了部分學生的成績,(滿分![]() 分)作為樣本,繪制了下面尚未完成的頻率分布表和頻率分布直方圖.
分)作為樣本,繪制了下面尚未完成的頻率分布表和頻率分布直方圖.
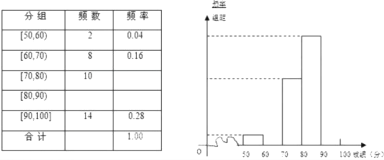
(1)填寫答題卡頻率分布表中的空格, 補全頻率分布直方圖, 并標出每個小矩形對應的縱軸數據;
(2)請你估算該年級的平均數及中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將甲、乙、丙、丁四名同學按一定順序排成一行,要求自左向右,且甲不排在第一,乙不排在第二,丙不排在第三,丁不排在第四,比如:“乙甲丁丙”是滿足要求的一種排法,試寫出他們四個人所有不同的排法.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要產生[-3,3]上的均勻隨機數y,現有[0,1]上的均勻隨機數x,則y可取為( )
A. -3x B. 3x
C. 6x-3 D. -6x-3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com