
【題目】已知函數(shù)f(x)=plnx+(p﹣1)x2+1.
(1)討論函數(shù)f(x)的單調(diào)性;
(2)當(dāng)P=1時,f(x)≤kx恒成立,求實(shí)數(shù)k的取值范圍;
(3)證明:1n(n+1)<1+ ![]() …+
…+ ![]() (n∈N+).
(n∈N+).
【答案】
(1)解:f(x)的定義域為(0,+∞),f′(x)= ![]() ,
,
當(dāng)p≥1時,f′(x)>0,故f(x)在(0,+∞)上單調(diào)遞增;
當(dāng)p≤0時,f′(x)<0,故f(x)在(0,+∞)上單調(diào)遞減;
當(dāng)0<p<1時,令f′(x)=0,解得x= ![]() .
.
則當(dāng)x ![]() 時,f′(x)>0;x
時,f′(x)>0;x ![]() 時,f′(x)<0,
時,f′(x)<0,
故f(x)在(0, ![]() )上單調(diào)遞增,在
)上單調(diào)遞增,在 ![]() 上單調(diào)遞減
上單調(diào)遞減
(2)解:∵x>0,
∴當(dāng)p=1時,f(x)≤kx恒成立1+lnx≤kxk≥ ![]() ,
,
令h(x)= ![]() ,則k≥h(x)max,
,則k≥h(x)max,
∵h(yuǎn)′(x)= ![]() =0,得x=1,
=0,得x=1,
且當(dāng)x∈(0,1),h′(x)>0;當(dāng)x∈(1,+∞),h′(x)<0;
所以h(x)在0,1)上遞增,在(1,+∞)上遞減,
所以h(x)max=h(1)=1,
故k≥1.
(3)證明:由(2)知,當(dāng)k=1時,有f(x)≤x,當(dāng)x>1時,f(x)<x,即lnx<x﹣1,
∴令x= ![]() ,則
,則 ![]() ,即
,即 ![]() ,
,
∴l(xiāng)n2﹣ln1<1, ![]() ,
, ![]()
相加得1n(n+1)<1+ ![]() …+
…+ ![]()
【解析】(1)利用導(dǎo)數(shù)來討論函數(shù)的單調(diào)性即可,具體的步驟是:(1)確定 f(x)的定義域;(2)求導(dǎo)數(shù)fˊ(x);(3)在函數(shù) 的定義域內(nèi)解不等式fˊ(x)>0和fˊ(x)<0;(4)確定 的單調(diào)區(qū)間.若在函數(shù)式中含字母系數(shù),往往要分類討論.(2)當(dāng)P=1時,f(x)≤kx恒成立,分離參數(shù)等價于k≥ ![]() ,利用導(dǎo)數(shù)求函數(shù)h(x)=
,利用導(dǎo)數(shù)求函數(shù)h(x)= ![]() 的最大值即可求得實(shí)數(shù)k的取值范圍;(3)由(2)知,當(dāng)k=1時,有f(x)≤x,當(dāng)x>1時,f(x)<x,即lnx<x﹣1,令x=
的最大值即可求得實(shí)數(shù)k的取值范圍;(3)由(2)知,當(dāng)k=1時,有f(x)≤x,當(dāng)x>1時,f(x)<x,即lnx<x﹣1,令x= ![]() ,則得到
,則得到 ![]() ,利用導(dǎo)數(shù)的運(yùn)算法則進(jìn)行化簡,然后再相加,即可證得結(jié)論.
,利用導(dǎo)數(shù)的運(yùn)算法則進(jìn)行化簡,然后再相加,即可證得結(jié)論.
【考點(diǎn)精析】利用利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性對題目進(jìn)行判斷即可得到答案,需要熟知一般的,函數(shù)的單調(diào)性與其導(dǎo)數(shù)的正負(fù)有如下關(guān)系: 在某個區(qū)間![]() 內(nèi),(1)如果
內(nèi),(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調(diào)遞增;(2)如果
在這個區(qū)間單調(diào)遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調(diào)遞減.
在這個區(qū)間單調(diào)遞減.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標(biāo)系中,已知三點(diǎn)O(0,0),A(2, ![]() ),B(2
),B(2 ![]() ,
, ![]() ).
).
(1)求經(jīng)過O,A,B的圓C1的極坐標(biāo)方程;
(2)以極點(diǎn)為坐標(biāo)原點(diǎn),極軸為x軸的正半軸建立平面直角坐標(biāo)系,圓C2的參數(shù)方程為 ![]() (θ是參數(shù)),若圓C1與圓C2外切,求實(shí)數(shù)a的值.
(θ是參數(shù)),若圓C1與圓C2外切,求實(shí)數(shù)a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列四個命題中,正確的個數(shù)是( )
①命題“存在x∈R,x2﹣x>0”的否定是“對于任意的x∈R,x2﹣x<0”;
②若函數(shù)f(x)在(2016,2017)上有零點(diǎn),則f(2016)f(2017)<0;
③在公差為d的等差數(shù)列{an}中,a1=2,a1 , a3 , a4成等比數(shù)列,則公差d為﹣ ![]() ;
;
④函數(shù)y=sin2x+cos2x在[0, ![]() ]上的單調(diào)遞增區(qū)間為[0,
]上的單調(diào)遞增區(qū)間為[0, ![]() ].
].
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() .
.
(1)求曲線y=f(x)在點(diǎn)(0,f(0))處的切線方程和函數(shù)f(x)的極值:
(2)若對任意x1 , x2∈[a,+∞),都有f(x1)﹣f(x2)≥﹣ ![]() 成立,求實(shí)數(shù)a的最小值.
成立,求實(shí)數(shù)a的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足:a1=1且an+1=2an+1,n∈N* , 設(shè)bn=n(an+1),則數(shù)列{bn}的前n項和Sn= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱 ![]() 中,平面
中,平面 ![]() 側(cè)面
側(cè)面 ![]() ,且
,且 ![]() .
. 
(1)求證: ![]() ;
;
(2)若直線 ![]() 與平面
與平面 ![]() 所成角的大小為
所成角的大小為 ![]() ,求銳二面角
,求銳二面角 ![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知 ![]() 分別是橢圓
分別是橢圓 ![]() 的左、右焦點(diǎn),離心率為
的左、右焦點(diǎn),離心率為 ![]() ,
, ![]() ,
, ![]() 分別是橢圓的上、下頂點(diǎn),
分別是橢圓的上、下頂點(diǎn), ![]() .
.
(Ⅰ)求橢圓 ![]() 的方程;
的方程;
(Ⅱ)過 ![]() (0,2)作直線
(0,2)作直線 ![]() 與
與 ![]() 交于
交于 ![]() 兩點(diǎn),求三角形
兩點(diǎn),求三角形 ![]() 面積的最大值(
面積的最大值( ![]() 是坐標(biāo)原點(diǎn)).
是坐標(biāo)原點(diǎn)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() sin2x+sinxcosx﹣
sin2x+sinxcosx﹣ ![]()
(1)求函數(shù)y=f(x)在[0, ![]() ]上的單調(diào)遞增區(qū)間;
]上的單調(diào)遞增區(qū)間;
(2)將函數(shù)y=f(x)的圖象向左平移 ![]() 個單位長度,再將圖象上所有點(diǎn)的橫坐標(biāo)伸長到原來的2倍(縱坐標(biāo)不變),得到函數(shù)y=g(x)的圖象,求證:存在無窮多個互不相同的整數(shù)x0 , 使得g(x0)>
個單位長度,再將圖象上所有點(diǎn)的橫坐標(biāo)伸長到原來的2倍(縱坐標(biāo)不變),得到函數(shù)y=g(x)的圖象,求證:存在無窮多個互不相同的整數(shù)x0 , 使得g(x0)> ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】上海市松江區(qū)天馬山上的“護(hù)珠塔”因其傾斜度超過意大利的比薩斜塔而號稱“世界第一斜塔”.興趣小組同學(xué)實(shí)施如下方案來測量塔的傾斜度和塔高:如圖,記O點(diǎn)為塔基、P點(diǎn)為塔尖、點(diǎn)P在地面上的射影為點(diǎn)H.在塔身OP射影所在直線上選點(diǎn)A,使仰角k∠HAP=45°,過O點(diǎn)與OA成120°的地面上選B點(diǎn),使仰角∠HPB=45°(點(diǎn)A,B,O都在同一水平面上),此時測得∠OAB=27°,A與B之間距離為33.6米.試求: 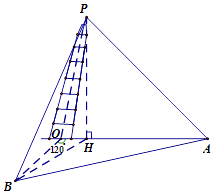
(1)塔高(即線段PH的長,精確到0.1米);
(2)塔身的傾斜度(即PO與PH的夾角,精確到0.1°).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com