
���}Ŀ���O(sh��)![]() ���溯��(sh��)��
���溯��(sh��)��![]() ��ż����(sh��)
��ż����(sh��)![]() ��������
��������![]() .
.
��1����![]() ��
��![]() �ı��_(d��)ʽ������(sh��)
�ı��_(d��)ʽ������(sh��)![]() ��ֵ��
��ֵ��
��2�����P(gu��n)��![]() �ķ���
�ķ���![]() �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)ǡ�Ѓɂ�(g��)���Ȍ�(sh��)������(sh��)
��(n��i)ǡ�Ѓɂ�(g��)���Ȍ�(sh��)������(sh��)![]() ��ȡֵ����
��ȡֵ����
���𰸡���1��![]() ֵ��?y��n)?/span>
ֵ��?y��n)?/span>![]() ��2��
��2��![]()
��������
��1���ɺ���(sh��)����ż�Կɵ�![]() ���ٽY(ji��)�ϗl���з��̽M��⣬�M(j��n)���ɵ�
���ٽY(ji��)�ϗl���з��̽M��⣬�M(j��n)���ɵ�![]() �����ú���(sh��)���{(di��o)�Կ����ֵ��
�����ú���(sh��)���{(di��o)�Կ����ֵ��
��2�����}��÷���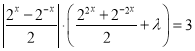 �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)ǡ�Ѓɂ�(g��)���Ȍ�(sh��)������
��(n��i)ǡ�Ѓɂ�(g��)���Ȍ�(sh��)������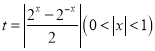 ���t�Ɍ������D(zhu��n)����
���t�Ɍ������D(zhu��n)����![]() �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)��Ψһ��(sh��)�������ú���(sh��)���{(di��o)����ú���(sh��)
��(n��i)��Ψһ��(sh��)�������ú���(sh��)���{(di��o)����ú���(sh��)![]() ��ֵ���M(j��n)���ɵó���(sh��)
��ֵ���M(j��n)���ɵó���(sh��)![]() ��ȡֵ����.
��ȡֵ����.
��1������֪![]() �٣�
�٣�
��![]() ��
��![]() ����
����![]() ��
��
��?y��n)?/span>![]() ���溯��(sh��)��
���溯��(sh��)��![]() ��ż����(sh��)��
��ż����(sh��)��
����![]() ����
����
(li��n)���٢ڿɵ�![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��
![]() ����(sh��)
����(sh��)![]() ��ֵ��?y��n)?/span>
��ֵ��?y��n)?/span>![]() ��
��
��2���}�⼴����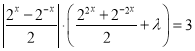 �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)ǡ�Ѓɂ�(g��)���Ȍ�(sh��)��.
��(n��i)ǡ�Ѓɂ�(g��)���Ȍ�(sh��)��.
�@Ȼ![]() ����ԓ���̵ĸ���������
����ԓ���̵ĸ���������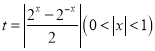
��![]() ��
��![]() ���tԭ���̿�׃�Ξ�
���tԭ���̿�׃�Ξ�![]()
��֪����(sh��)![]() ��ż����(sh��)�����څ^(q��)�g
��ż����(sh��)�����څ^(q��)�g![]() ��(n��i)���{(di��o)�f��������
��(n��i)���{(di��o)�f��������![]()
���}���D(zhu��n)���鷽��![]() �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)��Ψһ��(sh��)��(��?y��n)�ÿһ��(g��)
��(n��i)��Ψһ��(sh��)��(��?y��n)�ÿһ��(g��)![]() �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)ǡ�Ѓɂ�(g��)
��(n��i)ǡ�Ѓɂ�(g��)![]() ֵ�c֮����(y��ng)).
ֵ�c֮����(y��ng)).
��֪![]() �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)���{(di��o)�f�p��
��(n��i)���{(di��o)�f�p��
��![]() �r(sh��)��
�r(sh��)��![]() ��
��
����![]() ���˕r(sh��)ÿһ��(g��)
���˕r(sh��)ÿһ��(g��)![]() ���څ^(q��)�g
���څ^(q��)�g![]() ��(n��i)���҃H��һ��(g��)
��(n��i)���҃H��һ��(g��)![]() ֵ�c֮����(y��ng)).
ֵ�c֮����(y��ng)).
�C������������(sh��)![]() ��ȡֵ������
��ȡֵ������![]() .
.


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У����L��3�ľ���
�У����L��3�ľ���![]() �ɶ��c(di��n)
�ɶ��c(di��n)![]() ��
��![]() �քe��
�քe��![]() �S��
�S��![]() �S�ϻ��ӣ�
�S�ϻ��ӣ�![]() �ھ���
�ھ���![]() �ϣ���
�ϣ���![]() .
.
��1�����c(di��n)![]() ��܉�E
��܉�E![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)�c(di��n)![]() ��܉�E
��܉�E![]() ��һ�c(di��n)����ԭ�c(di��n)
��һ�c(di��n)����ԭ�c(di��n)![]() ��A
��A![]() ���ɗl�о��քe�c܉�E
���ɗl�о��քe�c܉�E![]() �����c(di��n)
�����c(di��n)![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��б�ʷքeӛ��
��б�ʷքeӛ��![]() ��
��![]() .
.
�����C��![]() ��
��
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�����FS��ABCD�У�����ABCD��߅�L��4�����Σ���BAD��60�㣬SA��SD��2![]() ���c(di��n)E����AD�����c(di��n)���c(di��n)F����SC�ϣ���
���c(di��n)E����AD�����c(di��n)���c(di��n)F����SC�ϣ���![]() ����SA//ƽ��BEF��
����SA//ƽ��BEF��
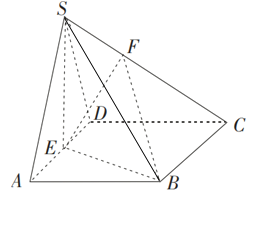
��1����(sh��)��(sh��)����ֵ��
��2���������FF��EBC���w�e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����������![]() �������c(di��n)̎���о�
�������c(di��n)̎���о�![]() ��������
��������![]() ��̎���о�
��̎���о�![]() ��ʹ��
��ʹ��![]() ���t��(sh��)��(sh��)
���t��(sh��)��(sh��)![]() ��ȡֵ������__________��
��ȡֵ������__________��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
�У�![]() �քe����
�քe����![]() �����c(di��n).��֪
�����c(di��n).��֪![]() ��
��![]() .
.
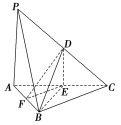
���C����1��ֱ��PA![]() ƽ��DEF��
ƽ��DEF��
��2��ƽ��BDE��ƽ��ABC.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ���{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g��
��2��������(sh��)![]() �ĈD������ƽ��
�ĈD������ƽ��![]() ��(g��)��λ�����ÈD��(y��ng)�ĺ���(sh��)��
��(g��)��λ�����ÈD��(y��ng)�ĺ���(sh��)��![]() .���P(gu��n)��
.���P(gu��n)��![]() �ķ���
�ķ���![]() �څ^(q��)�g
�څ^(q��)�g![]() ���Ѓɂ�(g��)����ȵČ�(sh��)������(sh��)��(sh��)
���Ѓɂ�(g��)����ȵČ�(sh��)������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�A![]() :
:![]() ,ֱ��
,ֱ��![]() .
.
(1)��ֱ��![]() �c�A
�c�A![]() ����,��
����,��![]() ��ֵ;
��ֵ;
(2)��ֱ��![]() �c�A
�c�A![]() ���ڲ�ͬ�ă��c(di��n)
���ڲ�ͬ�ă��c(di��n)![]() ,��(d��ng)��AOB���J�Ǖr(sh��),��k��ȡֵ����;
,��(d��ng)��AOB���J�Ǖr(sh��),��k��ȡֵ����;
(3)��![]() ,
,![]() ��ֱ��
��ֱ��![]() �ϵĄ��c(di��n),�^
�ϵĄ��c(di��n),�^![]() ���A
���A![]() �ăɗl�о�
�ăɗl�о�![]() ,���c(di��n)��
,���c(di��n)��![]() ,̽��:ֱ��
,̽��:ֱ��![]() �Ƿ��^���c(di��n)��
�Ƿ��^���c(di��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)��ԇ��
�r(sh��)��ԇ��![]() �Ć��{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2����![]() ��
��![]() ��(n��i)�ИOֵ��ԇ��
��(n��i)�ИOֵ��ԇ��![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ���������F![]() �У�����ABCD��ֱ�����Σ�
�У�����ABCD��ֱ�����Σ�![]() ��
��![]() ��
��![]() ���c(di��n)E��AD�����c(di��n)��
���c(di��n)E��AD�����c(di��n)��![]() ��
��![]() ƽ��ABCD����
ƽ��ABCD����![]()

��1�����C��![]() ��
��
��2������PC���Ƿ����һ�c(di��n)F��ʹ�����![]() ������ֵ��
������ֵ��![]() �������ڣ�Ո�ҳ��c(di��n)F��λ�ã��������ڣ�Ո�f�����ɣ�
�������ڣ�Ո�ҳ��c(di��n)F��λ�ã��������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com