
【題目】(本題滿分15分)如圖,在四棱錐![]() 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD, ![]() ,
,![]() ,E是BD的中點(diǎn).
,E是BD的中點(diǎn).

(Ⅰ)求證:EC//平面APD;
(Ⅱ)求BP與平面ABCD所成角的正切值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
【答案】(Ⅰ)詳見(jiàn)解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
試題分析:(Ⅰ)證明線面平行常用到的思路就是證明平面外的直線平行于平面內(nèi)的直線(Ⅱ)求BP與平面ABCD所成角首先找到斜線在平面中的射影![]() ,找到所求角
,找到所求角![]() ,通過(guò)求解三角形三邊得到角的大小(Ⅲ)利用三垂線定理作出二面角的平面角∠PGH,解
,通過(guò)求解三角形三邊得到角的大小(Ⅲ)利用三垂線定理作出二面角的平面角∠PGH,解![]() 三邊即可求得角的正弦值
三邊即可求得角的正弦值
試題解析:(Ⅰ)如圖,取PA中點(diǎn)F,連結(jié)EF、FD,
∵E是BP的中點(diǎn),∴EF//AB且![]() ,
,
又∵![]() ∴EF
∴EF![]() DC∴四邊形EFDC是平行四邊形,故得EC//FD 2分
DC∴四邊形EFDC是平行四邊形,故得EC//FD 2分
又∵EC![]() 平面PAD,FD
平面PAD,FD![]() 平面PAD∴EC//平面ADE 4分
平面PAD∴EC//平面ADE 4分
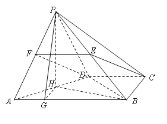
(Ⅱ)取AD中點(diǎn)H,連結(jié)PH,因?yàn)镻A=PD,
所以PH⊥AD
∵平面PAD⊥平面ABCD于AD ∴PH⊥面ABCD
∴HB是PB在平面ABCD內(nèi)的射影 ∴∠PBH是PB與平面ABCD所成角 6分
∵四邊形ABCD中,![]()
∴四邊形ABCD是直角梯形,![]()
設(shè)AB=2a,則![]() ,在
,在![]() 中,易得
中,易得![]() ,
,![]()
![]() ,又∵
,又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
∴在![]() 中,
中,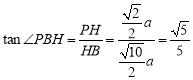 10分
10分
(Ⅲ)在平面ABCD內(nèi)過(guò)點(diǎn)H作AB的垂線交AB于G點(diǎn),連結(jié)PG,則HG是PG在平面ABCD上的射影,故PG⊥AB,所以∠PGH是二面角P-AB-D的平面角,由AB=2a 11分
![]() ,又
,又![]() ∴
∴![]() ,
,
在![]() 中,
中, 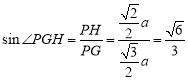
∴二面角P-AB-D的的正弦值為![]() 15分
15分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)f(x)=a﹣ ![]() ,x∈R,(其中a為常數(shù)).
,x∈R,(其中a為常數(shù)).
(1)若f(x)為奇函數(shù),求a的值;
(2)若不等式f(x)+a>0恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() :
: ![]() ,
, ![]() :
: ![]() (
(![]() ).
).
(1)若![]() ,
, ![]() 為假,
為假, ![]() 為真,求實(shí)數(shù)
為真,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() 是
是![]() 的充分條件,求實(shí)數(shù)
的充分條件,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知?jiǎng)訄A![]() 與圓
與圓![]() 相切,且與圓
相切,且與圓![]() 相內(nèi)切,記圓心
相內(nèi)切,記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)設(shè)![]() 為曲線
為曲線![]() 上的一個(gè)不在
上的一個(gè)不在![]() 軸上的動(dòng)點(diǎn),
軸上的動(dòng)點(diǎn), ![]() 為坐標(biāo)原點(diǎn),過(guò)點(diǎn)
為坐標(biāo)原點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 的平行線交曲線
的平行線交曲線![]() 于
于![]() 、
、![]() 兩個(gè)不同的點(diǎn),求
兩個(gè)不同的點(diǎn),求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下面結(jié)論正確的是( )
①一個(gè)數(shù)列的前三項(xiàng)是1,2,3,那么這個(gè)數(shù)列的通項(xiàng)公式![]() .
.
②由平面三角形的性質(zhì)推測(cè)空間四面體的性質(zhì),這是一種合理推理.
③在類(lèi)比時(shí),平面中的三角形與空間中的平行六面體作為類(lèi)比對(duì)象較為合適.
④“所有3的倍數(shù)都是9的倍數(shù),某數(shù)![]() 一定是9的倍數(shù),則
一定是9的倍數(shù),則![]() 一定是9的倍數(shù)”,這是三段論推理,但其結(jié)論是錯(cuò)誤的.
一定是9的倍數(shù)”,這是三段論推理,但其結(jié)論是錯(cuò)誤的.
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)f(x)=x2+2bx+c(b,c∈R).
(1)若函數(shù)y=f(x)的零點(diǎn)為﹣1和1,求實(shí)數(shù)b,c的值;
(2)若f(x)滿足f(1)=0,且關(guān)于x的方程f(x)+x+b=0的兩個(gè)實(shí)數(shù)根分別在區(qū)間(﹣3,﹣2),(0,1)內(nèi),求實(shí)數(shù)b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=a﹣ ![]() .
.
(1)若f(x)為奇函數(shù),求a的值.
(2)證明:不論a為何值f(x)在R上都單調(diào)遞增.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,已知橢圓C:![]() (m>0)的離心率為
(m>0)的離心率為![]() ,A,B分別為橢圓的左、右頂點(diǎn),F(xiàn)是其右焦點(diǎn),P是橢圓C上異于A、B的動(dòng)點(diǎn).
,A,B分別為橢圓的左、右頂點(diǎn),F(xiàn)是其右焦點(diǎn),P是橢圓C上異于A、B的動(dòng)點(diǎn).
(1)求m的值及橢圓的準(zhǔn)線方程;
(2)設(shè)過(guò)點(diǎn)B且與x軸的垂直的直線交AP于點(diǎn)D,當(dāng)直線AP繞點(diǎn)A轉(zhuǎn)動(dòng)時(shí),試判斷以BD為直徑的圓與直線PF的位置關(guān)系,并加以證明.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com