【題目】在直角坐標系xoy中，直線的參數方程為 
（t為參數），以原點O為極點，x軸的非負半軸為極軸建立極坐標系，曲線C的極坐標方程為 
．
（1）求曲線C的直角坐標方程，并指出其表示何種曲線；
（2）設直線l與曲線C交于A，B兩點，若點P的直角坐標為（1，0），試求當 
時，|PA|+|PB|的值．
【答案】
（1）解：曲線C2： 
，可以化為 
，ρ2=2ρcosθ﹣2ρsinθ，
因此，曲線C的直角坐標方程為x2+y2﹣2x+2y=0
它表示以（1，﹣1）為圓心、 
為半徑的圓
（2）解：當 
時，直線的參數方程為 
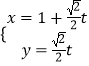（為參數）
點P（1，0）在直線上，且在圓C內，把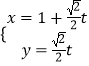
代入x2+y2﹣2x+2y=0中得 
設兩個實數根為t1，t2，則A，B兩點所對應的參數為t1，t2，
則 
，t1t2=﹣1）∴ 
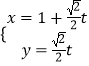【解析】（1）曲線C2： ，可以化為 ，ρ2=2ρcosθ﹣2ρsinθ，可得曲線C的直角坐標方程，并指出其表示何種曲線；（2）當 時，直線的參數方程為 （為參數），利用參數的幾何意義求當 時，|PA|+|PB|的值．
科目：高中數學 來源： 題型：
【題目】為豐富中學生的課余生活，增進中學生之間的交往與學習，某市甲乙兩所中學舉辦一次中學生圍棋擂臺賽．比賽規則如下，雙方各出3名隊員并預先排定好出場順序，雙方的第一號選手首先對壘，雙方的勝者留下進行下一局比賽，負者被淘汰出局，由第二號選手挑戰上一局獲勝的選手，依此類推，直到一方的隊員全部被淘汰，另一方算獲勝．假若雙方隊員的實力旗鼓相當（即取勝對手的概率彼此相等） （Ⅰ）在已知乙隊先勝一局的情況下，求甲隊獲勝的概率．
（Ⅱ）記雙方結束比賽的局數為ξ，求ξ的分布列并求其數學期望Eξ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四邊形ABCD為正方形，PD⊥平面ABCD，PD∥QA，QA=AB= 
PD．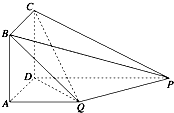
（1）證明：平面PQC⊥平面DCQ；
（2）求二面角Q﹣BP﹣C的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=（x+b）lnx，g（x）=alnx+ 
﹣x（a≠1），已知曲線y=f（x）在點（1，f（1））處的切線與直線x+2y=0垂直．
（1）求b的值；
（2）若對任意x≥1，都有g（x）＞ 
，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C的對邊分別為a，b，c
（1）若a，b，c成等比數列， 
，求 
的值；
（2）若A，B，C成等差數列，且b=2，設A=α，△ABC的周長為l，求l=f（α）的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設等差數列{an}的前n項和為Sn ， 已知a1=9，a2為整數，且Sn≤S5 ．
（1）求{an}的通項公式；
（2）設數列 
的前n項和為Tn ， 求證： 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現有1 000根某品種的棉花纖維，從中隨機抽取50根，纖維長度（單位：mm）的數據分組及各組的頻數見右上表，據此估計這1 000根中纖維長度不小于37.5 mm的根數是 ．
纖維長度 | 頻數 |
[22.5，25.5) | 3 |
[25.5，28.5) | 8 |
[28.5，31.5) | 9 |
[31.5，34.5) | 11 |
[34.5，37.5) | 10 |
[37.5，40.5) | 5 |
[40.5，43.5] | 4 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面直角坐標系xOy中，橢圓C： 
=1（a＞b＞0）的長軸長為2，拋物線E：x2=2y的準線與橢圓C相切．
（Ⅰ）求橢圓C的方程；
（Ⅱ）若直線l與橢圓C相交于A，B兩點且與拋物線E在第一象限相切于點P，線段AB的中點為D，直線OD與過P且垂直于x軸的直線交于點M，求 
的最小值及此時點P的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=aex（a≠0），g（x）=x2（Ⅰ）若曲線c1：y=f（x）與曲線c2：y=g（x）存在公切線，求a最大值．
（Ⅱ）當a=1時，F（x）=f（x）﹣bg（x）﹣cx﹣1，且F（2）=0，若F（x）在（0，2）內有零點，求實數b的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com