
【題目】已知點N在曲線![]() 上,直線
上,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,動點
,動點![]() 滿足
滿足![]() ,記點
,記點![]() 的軌跡為
的軌跡為![]()
(1)求![]() 的軌跡方程;
的軌跡方程;
(2)若過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 上 (
上 (![]() 為坐標原點),求證:
為坐標原點),求證:![]()
 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】曲線![]() 與兩坐標軸的交點都在圓
與兩坐標軸的交點都在圓![]() 上,圓
上,圓![]() 與
與![]() 軸正半軸、
軸正半軸、![]() 軸正半軸分別交于
軸正半軸分別交于![]() ,
,![]() 兩點.
兩點.
(Ⅰ)求圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 作直線
作直線![]() 與圓
與圓![]() 交于
交于![]() ,
,![]() 兩點,是否存在
兩點,是否存在![]() 使得
使得![]() 與
與![]() 共線,如果存在求直線
共線,如果存在求直線![]() 的方程,若不存在請說明理由.
的方程,若不存在請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
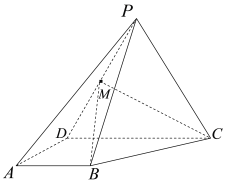
【題目】如圖,在四棱錐![]() 中,等邊三角形
中,等邊三角形![]() 所在的平面垂直于底面
所在的平面垂直于底面![]() ,
,![]() ,
, ![]() ,
,![]() 是棱
是棱![]() 的中點.
的中點.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判斷直線![]() 與平面
與平面![]() 的是否平行,并說明理由.
的是否平行,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將直角三角形![]() 沿斜邊上的高
沿斜邊上的高![]() 折成
折成![]() 的二面角,已知直角邊
的二面角,已知直角邊![]() ,
, ![]() ,那么下面說法正確的是( )
,那么下面說法正確的是( )
A. 平面![]() 平面
平面![]()
B. 四面體![]() 的體積是
的體積是![]()
C. 二面角![]() 的正切值是
的正切值是![]()
D. ![]() 與平面
與平面![]() 所成角的正弦值是
所成角的正弦值是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在以ABCDEF為頂點的五面體中,底面ABCD為菱形,∠ABC=120°,AB=AE=ED=2EF,EF![]() AB,點G為CD中點,平面EAD⊥平面ABCD.
AB,點G為CD中點,平面EAD⊥平面ABCD.
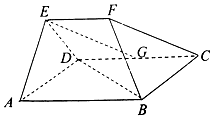
(1)證明:BD⊥EG;
(2)若三棱錐![]() ,求菱形ABCD的邊長.
,求菱形ABCD的邊長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,上頂點為
,上頂點為![]() ,
,![]() 的面積為1,且橢圓
的面積為1,且橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)點![]() 在橢圓上且位于第二象限,過點
在橢圓上且位于第二象限,過點![]() 作直線
作直線![]() ,過點
,過點![]() 作直線
作直線![]() ,若直線
,若直線![]() 的交點
的交點![]() 恰好也在橢圓
恰好也在橢圓![]() 上,求點
上,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年10月28日,重慶公交車墜江事件震驚全國,也引發了廣大群眾的思考——如何做一個文明的乘客.全國各地大部分社區組織居民學習了文明乘車規范.![]() 社區委員會針對居民的學習結果進行了相關的問卷調查,并將得到的分數整理成如圖所示的統計圖.
社區委員會針對居民的學習結果進行了相關的問卷調查,并將得到的分數整理成如圖所示的統計圖.
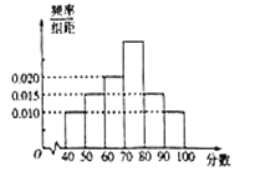
(Ⅰ)求得分在![]() 上的頻率;
上的頻率;
(Ⅱ)求![]() 社區居民問卷調查的平均得分的估計值;(同一組中的數據以這組數據所在區間中點的值作代表)
社區居民問卷調查的平均得分的估計值;(同一組中的數據以這組數據所在區間中點的值作代表)
(Ⅲ)以頻率估計概率,若在全部參與學習的居民中隨機抽取5人參加問卷調查,記得分在![]() 間的人數為
間的人數為![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com