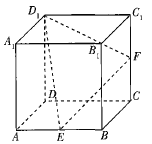
【題目】如圖，在棱長為12的正方體
中，已知E，F分別為棱AB，
的中點，若過點
，E，F的平面截正方體所得的截面為一個多邊形，則該多邊形的周長為________，該多邊形與平面
，ABCD的交線所成角的余弦值為________．
【答案】
【解析】
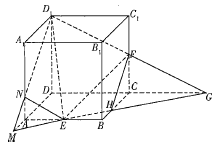
延長DC，與
的延長線交于點G，連接EG，交BC于點H，延長GE，與DA的延長線交于點M，連接
，交
于點N．連接NE，FH，作出截面多邊形，由此易求該截面多邊形的周長；多邊形與平面
，ABCD的交線分別為
與
，由面面平行的性質定理得
∥，則
為多邊形與平面，ABCD的交線所成的角或其補角，利用余弦定理計算
即可.
如圖，延長DC，與的延長線交于點G，連接EG，交BC于點H，延長GE，與DA的
延長線交于點M，連接，交于點N．連接NE，FH，
因為正方體
的棱長為12，
所以
．
因為
∥
，
所以
，
所以
，
所以
，
同理可得
，
所以
，
所以
，
，
所以
，
．
易知
，所以
，
又
，解得
，
所以
，
，
則該多邊形的周長為
．
由面面平行的性質定理得∥，
則為多邊形與平面，ABCD的交線所成的角或其補角．
因為
，所以
，
所以該多邊形與平面，ABCD的交線所成角的余弦值為．
故答案為：；
小學學習好幫手系列答案
小學同步三練核心密卷系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的離心率為
，設直線
過橢圓的上頂點和右焦點，坐標原點
到直線的距離為2.
（1）求橢圓的方程.
（2）過點
且斜率不為零的直線交橢圓于
，
兩點，在
軸的正半軸上是否存在定點
，使得直線
，
的斜率之積為非零的常數？若存在，求出定點的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】哈三中總務處的老師要購買學校教學用的粉筆，并且有非常明確的判斷一盒粉筆是“優質產品”和“非優質產品”的方法.某品牌的粉筆整箱出售，每箱共有20盒，根據以往的經驗，其中會有某些盒的粉筆為非優質產品，其余的都為優質產品.并且每箱含有0，1，2盒非優質產品粉筆的概率為0.7，0.2和0.1.為了購買該品牌的粉筆，校總務主任設計了一種購買的方案：欲買一箱粉筆,隨機查看該箱的4盒粉筆，如果沒有非優質產品，則購買，否則不購買.設“買下所查看的一箱粉筆”為事件
，“箱中有
件非優質產品”為事件
.
（1）求
，
，
；
（2）隨機查看該品牌粉筆某一箱中的四盒，設
為非優質產品的盒數，求的分布列及期望；
（3）若購買100箱該品牌粉筆，如果按照主任所設計方案購買的粉筆中，箱中每盒粉筆都是優質產品的箱數的期望比隨機購買的箱中每盒粉筆都是優質產品的箱數的期望大10，則所設計的方案有效.討論該方案是否有效.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為進一步深化“平安校園”創建活動，加強校園安全教育宣傳，某高中對該校學生進行了安全教育知識測試（滿分100分），并從中隨機抽取了200名學生的成績，經過數據分析得到如圖1所示的頻數分布表，并繪制了得分在
以及
的莖葉圖，分別如圖23所示．
成績 |
|
|
|
|
|
|
|
頻數 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
圖1
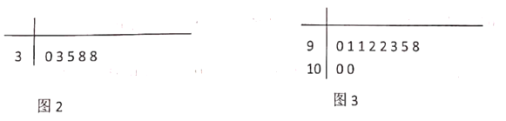
（1）求這200名同學得分的平均數；（同組數據用區間中點值作代表）
（2）如果變量
滿足
且
，則稱變量“近似滿足正態分布
的概率分布”．經計算知樣本方差為210，現在取
和
分別為樣本平均數和方差，以樣本估計總體，將頻率視為概率，如果該校學生的得分“近似滿足正態分布的概率分布”，則認為該校的校園安全教育是成功的，否則視為不成功．試判斷該校的安全教育是否成功，并說明理由．
（3）學校決定對90分及以上的同學進行獎勵，為了體現趣味性，采用抽獎的方式進行，其中得分不低于94的同學有兩次抽獎機會，低于94的同學只有一次抽獎機會，每次抽獎的獎金及對應的概率分別為：
獎金 | 50 | 100 |
概率 |
|
|
現在從不低于90同學中隨機選一名同學，記其獲獎金額為
，以樣本估計總體，將頻率視為概率，求的分布列和數學期望．
（參考數據：
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
，圓
：
，一動圓在
軸右側與軸相切，同時與圓相外切，此動圓的圓心軌跡為曲線
，橢圓與曲線有相同的焦點.
（1）求曲線的方程；
（2）設曲線與橢圓相交于第一象限點
，且
，求橢圓的標準方程；
（3）在（2）的條件下，如果橢圓的左頂點為
，過且垂直于
軸的直線與橢圓交于
，
兩點，直線
，
與直線
：
分別交于
，
兩點，證明：四邊形
的對角線的交點是橢圓的右頂點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面ABCD為矩形，
，
，側面SAD是以AD為斜邊的等腰直角三角形，且平面
平面ABCD，M，N分別為AD，SC的中點．
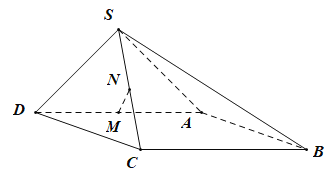
（1）求證：
平面SAB．
（2）求直線BN與平面SAB所成角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓：
的四個頂點圍成的四邊形的面積為
，原點到直線
的距離為
.
（1）求橢圓
的方程；
（2）已知定點
，是否存在過
的直線
，使與橢圓交于
，
兩點，且以
為直徑的圓過橢圓的左頂點？若存在，求出的方程：若不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
