
【題目】已知數(shù)列{an}滿(mǎn)足a1=1,且anan+1=2n , n∈N* , 則數(shù)列{an}的通項(xiàng)公式為( )
A.an=( ![]() )n﹣1
)n﹣1
B.an=( ![]() )n
)n
C.an= ![]()
D.an= ![]()
【答案】D
【解析】解:∵數(shù)列{an}滿(mǎn)足a1=1,且anan+1=2n , n∈N* ,
∴an+1an+2=2n+1 ,
兩式相比得 ![]() =2,即數(shù)列中的奇數(shù)項(xiàng)是以1為首項(xiàng),2為公比的等比數(shù)列,
=2,即數(shù)列中的奇數(shù)項(xiàng)是以1為首項(xiàng),2為公比的等比數(shù)列,
即當(dāng)n是奇數(shù)時(shí),an=( ![]() )n﹣1 ,
)n﹣1 ,
偶數(shù)項(xiàng)是以a2=2為首項(xiàng),2為公比的等比數(shù)列,
則當(dāng)n是偶數(shù)時(shí),an=2( ![]() )n﹣1=(
)n﹣1=( ![]() )n ,
)n ,
故數(shù)列的通項(xiàng)公式an= ![]() ,
,
故選:D.
【考點(diǎn)精析】本題主要考查了數(shù)列的定義和表示和數(shù)列的通項(xiàng)公式的相關(guān)知識(shí)點(diǎn),需要掌握數(shù)列中的每個(gè)數(shù)都叫這個(gè)數(shù)列的項(xiàng).記作an,在數(shù)列第一個(gè)位置的項(xiàng)叫第1項(xiàng)(或首項(xiàng)),在第二個(gè)位置的叫第2項(xiàng),……,序號(hào)為n的項(xiàng)叫第n項(xiàng)(也叫通項(xiàng))記作an;如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個(gè)公式表示,那么這個(gè)公式就叫這個(gè)數(shù)列的通項(xiàng)公式才能正確解答此題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=2cos2ωx+ ![]() sin2ωx(ω>0)的最小正周期為π,給出下列四個(gè)命題:
sin2ωx(ω>0)的最小正周期為π,給出下列四個(gè)命題:
①f(x)的最大值為3;
②將f(x)的圖象向左平移 ![]() 后所得的函數(shù)是偶函數(shù);
后所得的函數(shù)是偶函數(shù);
③f(x)在區(qū)間[﹣ ![]() ,
, ![]() ]上單調(diào)遞增;
]上單調(diào)遞增;
④f(x)的圖象關(guān)于直線(xiàn)x= ![]() 對(duì)稱(chēng).
對(duì)稱(chēng).
其中正確說(shuō)法的序號(hào)是( )
A.②③
B.①④
C.①②④
D.①③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商場(chǎng)對(duì)顧客實(shí)行購(gòu)物優(yōu)惠活動(dòng),規(guī)定一次購(gòu)物付款總額:
(1)如果不超過(guò)200元,則不給予優(yōu)惠;
(2)如果超過(guò)200元但不超過(guò)500元,則按標(biāo)價(jià)給予9折優(yōu)惠;
(3)如果超過(guò)500元,其500元內(nèi)的按第(2)條給予優(yōu)惠,超過(guò)500元的部分給予7折優(yōu)惠.
某人單獨(dú)購(gòu)買(mǎi)A,B商品分別付款168元和423元,假設(shè)他一次性購(gòu)買(mǎi)A,B兩件商品,則應(yīng)付款是
A. 413.7元 B. 513.7元 C. 546.6元 D. 548.7元
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB是⊙O的一條切線(xiàn),切點(diǎn)為B,直線(xiàn)ADE、CFD、CGE都是⊙O的割線(xiàn),已知AC=AB. 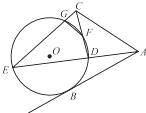
(1)若CG=1,CD=4.求 ![]() 的值.
的值.
(2)求證:FG∥AC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 是定義在實(shí)數(shù)集
是定義在實(shí)數(shù)集![]() 上的奇函數(shù),當(dāng)
上的奇函數(shù),當(dāng)![]() 時(shí),
時(shí),![]()
![]() ,若集合
,若集合![]() ,則實(shí)數(shù)
,則實(shí)數(shù)![]() 的取值范圍是______.
的取值范圍是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中,已知拋物線(xiàn)
中,已知拋物線(xiàn)![]() :
:![]() ,拋物線(xiàn)
,拋物線(xiàn)![]() 的準(zhǔn)線(xiàn)與
的準(zhǔn)線(xiàn)與![]() 交于點(diǎn)
交于點(diǎn)![]() .
.
(1)過(guò)![]() 作曲線(xiàn)
作曲線(xiàn)![]() 的切線(xiàn),設(shè)切點(diǎn)為
的切線(xiàn),設(shè)切點(diǎn)為![]() ,
, ![]() ,證明:以
,證明:以![]() 為直徑的圓經(jīng)過(guò)點(diǎn)
為直徑的圓經(jīng)過(guò)點(diǎn)![]() ;
;
(2)過(guò)點(diǎn)![]() 作互相垂直的兩條直線(xiàn)
作互相垂直的兩條直線(xiàn)![]() 、
、![]() ,
, ![]() 與曲線(xiàn)
與曲線(xiàn)![]() 交于
交于![]() 、
、![]() 兩點(diǎn),
兩點(diǎn), ![]() 與曲線(xiàn)
與曲線(xiàn)![]() 交于
交于![]() 、
、![]() 兩點(diǎn),線(xiàn)段
兩點(diǎn),線(xiàn)段![]() ,
, ![]() 的中點(diǎn)分別為
的中點(diǎn)分別為![]() 、
、![]() ,試討論直線(xiàn)
,試討論直線(xiàn)![]() 是否過(guò)定點(diǎn)?若過(guò),求出定點(diǎn)的坐標(biāo);若不過(guò),請(qǐng)說(shuō)明理由.
是否過(guò)定點(diǎn)?若過(guò),求出定點(diǎn)的坐標(biāo);若不過(guò),請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)f(x)=x3+mlog2(x+ ![]() )(m∈R,m>0),則不等式f(m)+f(m2﹣2)≥0的解是 . (注:填寫(xiě)m的取值范圍)
)(m∈R,m>0),則不等式f(m)+f(m2﹣2)≥0的解是 . (注:填寫(xiě)m的取值范圍)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)![]() .
.
(1)當(dāng)q=1時(shí),求f(x)在[﹣1,9]上的值域;
(2)問(wèn):是否存在常數(shù)q(0<q<10),使得當(dāng)x∈[q,10]時(shí),f(x)的最小值為﹣51?若存在,求出q的值,若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】公司生產(chǎn)一種電子儀器的固定成本為20000元,每生產(chǎn)一臺(tái)儀器需增加投入100元,已知總收益滿(mǎn)足函數(shù):
其中  x 是儀器的月產(chǎn)量.
x 是儀器的月產(chǎn)量.
(1)將利潤(rùn)![]() 表示為月產(chǎn)量
表示為月產(chǎn)量 
![]() 的函數(shù);
的函數(shù);
(2)當(dāng)月產(chǎn)量 
![]() 為何值時(shí),公司所獲利潤(rùn)最大?最大利潤(rùn)是多少元?(總收益=總成本+利潤(rùn))
為何值時(shí),公司所獲利潤(rùn)最大?最大利潤(rùn)是多少元?(總收益=總成本+利潤(rùn))![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com