
【題目】已知橢圓![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,橢圓
上,橢圓![]() 的離心率是
的離心率是![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)點![]() 為橢圓長軸的左端點,
為橢圓長軸的左端點,![]() 為橢圓上異于橢圓
為橢圓上異于橢圓![]() 長軸端點的兩點,記直線
長軸端點的兩點,記直線![]() 斜率分別為
斜率分別為![]() ,若
,若![]() ,請判斷直線
,請判斷直線![]() 是否過定點?若過定點,求該定點坐標(biāo),若不過定點,請說明理由.
是否過定點?若過定點,求該定點坐標(biāo),若不過定點,請說明理由.
【答案】(1)![]() (2)過定點
(2)過定點![]()
【解析】
(1)由點M(﹣1,![]() )在橢圓C上,且橢圓C的離心率是
)在橢圓C上,且橢圓C的離心率是![]() ,列方程組求出a=2,b
,列方程組求出a=2,b![]() ,由此能求出橢圓C的標(biāo)準(zhǔn)方程.
,由此能求出橢圓C的標(biāo)準(zhǔn)方程.
(2)設(shè)點P,Q的坐標(biāo)分別為(x1,y1),(x2,y2),當(dāng)直線PQ的斜率存在時,設(shè)直線PQ的方程為y=kx+m,聯(lián)立 ,得:(4k2+3)x2+8kmx+(4m2﹣12)=0,利用根的判別式、韋達(dá)定理,結(jié)合已知條件得直線PQ的方程過定點(1,0);再驗證直線PQ的斜率不存在時,同樣推導(dǎo)出x0=1,從而直線PQ過(1,0).由此能求出直線PQ過定點(1,0).
,得:(4k2+3)x2+8kmx+(4m2﹣12)=0,利用根的判別式、韋達(dá)定理,結(jié)合已知條件得直線PQ的方程過定點(1,0);再驗證直線PQ的斜率不存在時,同樣推導(dǎo)出x0=1,從而直線PQ過(1,0).由此能求出直線PQ過定點(1,0).
(1)由點![]() 在橢圓
在橢圓![]() 上,且橢圓
上,且橢圓![]() 的離心率是
的離心率是![]() ,
,
可得 ,
,
可解得:
故橢圓![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() .
.
(2)設(shè)點![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,
,
(ⅰ)當(dāng)直線![]() 斜率不存在時,由題意知,直線方程和曲線方程聯(lián)立得:
斜率不存在時,由題意知,直線方程和曲線方程聯(lián)立得:![]() ,
,![]() ,
,
(ⅱ)當(dāng)直線![]() 的斜率存在時,設(shè)直線
的斜率存在時,設(shè)直線![]() 的方程為
的方程為![]() ,
,
聯(lián)立 ,消去
,消去![]() 得:
得:![]() ,
,
由![]() ,有
,有![]() ,
,
由韋達(dá)定理得:![]() ,
,![]() ,
,
故![]() ,可得:
,可得:![]() ,
,
可得:![]() ,
,
整理為:![]() ,
,
故有![]() ,
,
化簡整理得:![]() ,解得:
,解得:![]() 或
或![]() ,
,
當(dāng)![]() 時直線
時直線![]() 的方程為
的方程為![]() ,即
,即![]() ,過定點
,過定點![]() 不合題意,
不合題意,
當(dāng)![]() 時直線
時直線![]() 的方程為
的方程為![]() ,即
,即![]() ,過定點
,過定點![]() ,
,
綜上,由(ⅰ)(ⅱ)知,直線![]() 過定點
過定點![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】為維護(hù)交通秩序,防范電動自行車被盜,天津市公安局決定,開展二輪電動自行車免費登記、上牌照工作.電動自行車牌照分免費和收費(安裝防盜裝置)兩大類,群眾可以 自愿選擇安裝.已知甲、乙、丙三個不同類型小區(qū)的人數(shù)分別為15000,15000,20000.交管部門為了解社區(qū)居民意愿,現(xiàn)采用分層抽樣的方法從中抽取10人進(jìn)行電話訪談.
(Ⅰ)應(yīng)從甲小區(qū)和丙小區(qū)的居民中分別抽取多少人?
(Ⅱ)設(shè)從甲小區(qū)抽取的居民為![]() ,丙小區(qū)抽取的居民為
,丙小區(qū)抽取的居民為![]() .現(xiàn)從甲小區(qū)和丙小區(qū)已抽取的居民中隨機(jī)抽取2人接受問卷調(diào)查.
.現(xiàn)從甲小區(qū)和丙小區(qū)已抽取的居民中隨機(jī)抽取2人接受問卷調(diào)查.
(ⅰ)試用所給字母列舉出所有可能的抽取結(jié)果;
(ⅱ)設(shè)![]() 為事件“抽取的2人來自不同的小區(qū)”,求事件
為事件“抽取的2人來自不同的小區(qū)”,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動,點
軸滾動,點![]() 恰好經(jīng)過原點.設(shè)頂點
恰好經(jīng)過原點.設(shè)頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則對函數(shù)
,則對函數(shù)![]() 有下列判斷:①函數(shù)
有下列判斷:①函數(shù)![]() 是偶函數(shù);②對任意的
是偶函數(shù);②對任意的![]() ,都有
,都有![]() ;③函數(shù)
;③函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減;④函數(shù)
上單調(diào)遞減;④函數(shù)![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判斷正確的序號是__________.
.其中判斷正確的序號是__________.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,已知![]() 為圓
為圓![]() 的直徑,點
的直徑,點![]() 為線段
為線段![]() 上一點,且
上一點,且![]() ,點
,點![]() 為圓
為圓![]() 上一點,且
上一點,且![]() .點
.點![]() 在圓
在圓![]() 所在平面上的正投影為點
所在平面上的正投影為點![]() ,
,![]() .
.

(1)求證:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=![]() .
.
(1)判斷函數(shù)在區(qū)間(-1,+∞)上的單調(diào)性,并用定義證明你的結(jié)論;
(2)求該函數(shù)在區(qū)間[2,4]上的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)已知sin(-π+θ)+2cos(3π-θ)=0,則![]() ;
;
(2)已知![]() .
.
①化簡f(α);
②若f(α)![]() ,且
,且![]() ,求cos α-sin α的值;
,求cos α-sin α的值;
③若![]()
![]() ,求f(α)的值.
,求f(α)的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
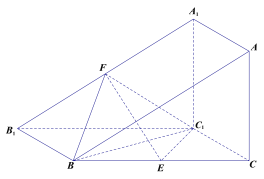
【題目】如圖,三棱柱![]() 的側(cè)面
的側(cè)面![]() 是平行四邊形,
是平行四邊形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分別是
分別是![]() 的中點.
的中點.
(1)求證:![]() 平面
平面![]() ;
;
(2)當(dāng)側(cè)面![]() 是正方形,且
是正方形,且![]() 時,
時,
(ⅰ)求二面角![]() 的大小;
的大小;
(ⅱ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,指出點
?若存在,指出點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() (其中
(其中![]() )的部分圖象如圖所示,把函數(shù)
)的部分圖象如圖所示,把函數(shù)![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,再向下平移1個單位,得到函數(shù)
個單位長度,再向下平移1個單位,得到函數(shù)![]() 的圖像.
的圖像.

(1)當(dāng)![]() 時,求
時,求![]() 的值域
的值域
(2)令![]() ,若對任意
,若對任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com