
【題目】已知![]() =(sinx,cosx),
=(sinx,cosx),![]() =(cosφ,sinφ)(|φ|<
=(cosφ,sinφ)(|φ|<![]() ).函數
).函數
f(x)=![]()
![]() 且f(
且f(![]() -x)=f(x).
-x)=f(x).
(Ⅰ)求f(x)的解析式及單調遞增區間;
(Ⅱ)將f(x)的圖象向右平移![]() 單位得g(x)的圖象,若g(x)+1≤ax+cosx在x∈[0,
單位得g(x)的圖象,若g(x)+1≤ax+cosx在x∈[0, ![]() ]上恒成立,求實數a的取值范圍.
]上恒成立,求實數a的取值范圍.
【答案】(Ⅰ)f(x)=sin(x+![]() ),
),![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】試題分析:(1)利用向量的坐標運算得到![]() ,再由f(
,再由f(![]() -x)=f(x)可知函數f(x)的圖象關于直線x=
-x)=f(x)可知函數f(x)的圖象關于直線x=![]() 對稱,所以
對稱,所以![]() +φ=
+φ=![]() +kπ,進而得到φ=
+kπ,進而得到φ=![]() ,利用三角函數的性質求解單調區間即可;
,利用三角函數的性質求解單調區間即可;
(2)將f(x)的圖象向右平移![]() 單位得g(x)= sinx,即sinx+1≤ax+cosx在x∈[0,
單位得g(x)= sinx,即sinx+1≤ax+cosx在x∈[0,![]() ]上恒成立,利用數形結合分別研究h(x)=sinx-cosx和φ(x)= ax—1即可.
]上恒成立,利用數形結合分別研究h(x)=sinx-cosx和φ(x)= ax—1即可.
試題解析:
(Ⅰ)∵f(x)=![]()
![]() =sinxcosφ+cosxsinφ=sin(x+φ),
=sinxcosφ+cosxsinφ=sin(x+φ),
再由f(![]() -x)=f(x)可知函數f(x)的圖象關于直線x=
-x)=f(x)可知函數f(x)的圖象關于直線x=![]() 對稱,
對稱,
∴![]() +φ=
+φ=![]() +kπ,k∈Z,又|φ|<
+kπ,k∈Z,又|φ|<![]() ,∴φ=
,∴φ=![]()
∴f(x)=sin(x+![]() ),
),
由2kπ-![]() ≤ x+
≤ x+![]() ≤2kπ+
≤2kπ+![]() 可得2kπ-
可得2kπ-![]() ≤x≤ 2kπ+
≤x≤ 2kπ+![]() ,
,
∴函數的遞增區間為[2kπ-![]() ,2kπ+
,2kπ+![]() ],k∈Z;
],k∈Z;
(Ⅱ)由圖象平移易知g(x)=sinx,即sinx+1≤ax+cosx在x∈[0,![]() ]上恒成立.
]上恒成立.
也即sinx-cosx≤ax-1在x∈[0,![]() ]上恒成立.
]上恒成立.
令h(x)=sinx-cosx=![]() sin(x-
sin(x-![]() ),x∈[0,
),x∈[0,![]() ];
];
φ(x)= ax-1
如下圖:h(x)的圖象在φ(x)圖象的下方,

則: a ≥kAB=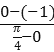 =
=![]() ,故
,故![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集為[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求證:ax+by+cz≤1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們知道:人們對聲音有不同的感覺,這與它的強度有關系.聲音的強度![]() 用瓦/米2 (
用瓦/米2 (![]() )表示,但在實際測量時,常用聲音的強度水平
)表示,但在實際測量時,常用聲音的強度水平![]() 表示,它們滿足以下公式:
表示,它們滿足以下公式: ![]() (單位為分貝,
(單位為分貝, ![]() ,其中
,其中![]() ,這是人們平均能聽到的最小強度,是聽覺的開端).回答以下問題:
,這是人們平均能聽到的最小強度,是聽覺的開端).回答以下問題:
(1)樹葉沙沙聲的強度是![]() ,耳語的強度是
,耳語的強度是![]() ,恬靜的無線電廣播的強度是
,恬靜的無線電廣播的強度是![]() ,試分別求出它們的強度水平;
,試分別求出它們的強度水平;
(2)某一新建的安靜小區規定:小區內公共場所的聲音的強度水平必須保持在50分貝以下,試求聲音強度![]() 的范圍為多少?
的范圍為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
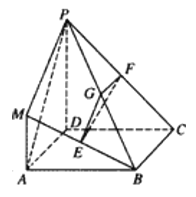
【題目】在如圖所示的幾何體中,四邊形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分別為
分別為![]() 的中點,且
的中點,且![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 與四棱錐
與四棱錐![]() 的體積之比.
的體積之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是R上的偶函數,且在[0,+∞)上單調遞增,則f(-2),f(3),f(-![]() )的大小順序是:( )
)的大小順序是:( )
A. f(-![]() )>f(3)>f(-2) B. f(-
)>f(3)>f(-2) B. f(-![]() ) >f(-2)>f(3)
) >f(-2)>f(3)
C. f(-2)>f(3)> f(-![]() ) D. f(3)>f(-2)> f(-
) D. f(3)>f(-2)> f(-![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1處有極值10,求a,b的值;
(II)若當a=-1時,f(x)<0在x∈[1,2]恒成立,求b的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程并指出其形狀;
的直角坐標方程并指出其形狀;
(2)設![]() 是曲線
是曲線![]() 上的動點,求
上的動點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com