
【題目】如圖,在三棱錐![]() 中,△ABC是等邊三角形,AB⊥AD,CB⊥CD,點P是AC的中點,記△BPD、△ABD的面積分別為
中,△ABC是等邊三角形,AB⊥AD,CB⊥CD,點P是AC的中點,記△BPD、△ABD的面積分別為![]() ,
,![]() ,二面角A-BD-C的大小為
,二面角A-BD-C的大小為![]() ,
,
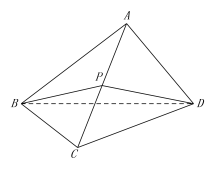
證明:(Ⅰ)平面ACD![]() 平面BDP;
平面BDP;
(Ⅱ)![]() .
.
【答案】(Ⅰ)見解析(Ⅱ)見解析
【解析】
(Ⅰ)由題意可知Rt△BAD≌Rt△BCD,∴AD=CD,又P是AC的中點,∴PB⊥AC,PD⊥AC,可得AC⊥平面BDP ,結合面面垂直的判定定理即可得證。
(Ⅱ)作AM⊥ BD,M為垂足,連接PM,CM.可得AC⊥PM,AC⊥BD,所以BD⊥CM,則∠AMC就是二面角A-BD-C的平面角,即∠AMC=![]() . 可求出
. 可求出![]() 與
與![]() 的關系,即可得證。
的關系,即可得證。
(Ⅰ)證明:∵△ABC是等邊三角形,AB⊥AD,CB⊥CD,
∴Rt△BAD≌Rt△BCD,∴AD=CD.
∵點P是AC的中點,∴PB⊥AC,PD⊥AC,
又![]() =P,
=P,![]() 平面BDP,
平面BDP,![]() 平面BDP,
平面BDP,
∴AC⊥平面BDP,
∵![]() 平面ACD,∴平面ACD⊥平面BDP.
平面ACD,∴平面ACD⊥平面BDP.
(Ⅱ)證明:作AM⊥ BD,M為垂足,連接PM,CM.
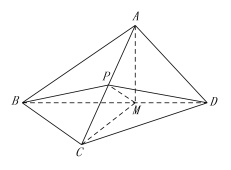
由(1)知AC⊥平面BDP,則AC⊥PM,AC⊥BD,
∵![]() ,∴BD⊥平面ACM,
,∴BD⊥平面ACM,
∴BD⊥CM,則∠AMC就是二面角A-BD-C的平面角,即∠AMC=![]() .
.
又P為AC的中點,PM⊥AC,則∠AMP=![]() ,
,
所以 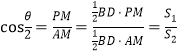 ,
,
所以![]() .
.


 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() .如果數列
.如果數列![]() 滿足
滿足![]() ,
, ![]() ,其中
,其中![]() ,則稱
,則稱![]() 為
為![]() 的“陪伴數列”.
的“陪伴數列”.
(Ⅰ)寫出數列![]() 的“陪伴數列”
的“陪伴數列”![]() ;
;
(Ⅱ)若![]() 的“陪伴數列”是
的“陪伴數列”是![]() .試證明:
.試證明: ![]() 成等差數列.
成等差數列.
(Ⅲ)若![]() 為偶數,且
為偶數,且![]() 的“陪伴數列”是
的“陪伴數列”是![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的方程是:
的方程是: ![]() ,以坐標原點為極點,
,以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)設過原點的直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左右焦點分別
的左右焦點分別![]()
![]() ,過
,過![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 交橢圓于
交橢圓于![]() 兩點,滿足
兩點,滿足![]() .
.
(1)求橢圓![]() 的離心率.
的離心率.
(2)![]() 是橢圓
是橢圓![]() 短軸的兩個端點,設點
短軸的兩個端點,設點![]() 是橢圓
是橢圓![]() 上一點(異于橢圓
上一點(異于橢圓![]() 的頂點),直線
的頂點),直線![]() 分別與
分別與![]() 軸相交于
軸相交于![]() 兩點,
兩點,![]() 為坐標原點,若
為坐標原點,若![]() ,求橢圓
,求橢圓![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查某地區老年人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
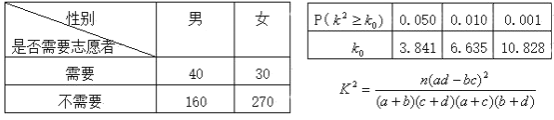
(1)估計該地區老年人中,需要志愿者提供幫助的老年人的比例;
(2)能否有99%的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,-2),橢圓E: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,F是橢圓E的右焦點,直線AF的斜率為
,F是橢圓E的右焦點,直線AF的斜率為![]() ,O為坐標原點.
,O為坐標原點.
(1)求E的方程;
(2)設過點A的動直線l與E相交于P,Q兩點.當△OPQ的面積最大時,求l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點,焦點在![]() 軸上的橢圓
軸上的橢圓![]() 的離心率為
的離心率為![]() ,且經過點
,且經過點![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)是否存在過點![]() 的直線
的直線![]() 與
與![]() 相交于不同的兩點
相交于不同的兩點![]() ,滿足
,滿足![]() ?
?
若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 都是各項不為零的數列,且滿足
都是各項不為零的數列,且滿足![]() ,
,![]() ,其中
,其中![]() 是數列
是數列![]() 的前
的前![]() 項和,
項和,![]() 是公差為
是公差為![]() 的等差數列.
的等差數列.
(1)若數列![]() 的通項公式分別為
的通項公式分別為![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)若![]() (
(![]() 是不為零的常數),求證:數列
是不為零的常數),求證:數列![]() 是等差數列;
是等差數列;
(3)若![]() (
(![]() 為常數,
為常數,![]() ),
),![]() (
(![]() ,
,![]() ),對任意
),對任意![]() ,
,![]() ,求出數列
,求出數列![]() 的最大項(用含
的最大項(用含![]() 式子表達).
式子表達).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com