
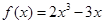 .
.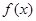 在區(qū)間
在區(qū)間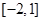 上的最大值;
上的最大值;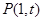 存在3條直線與曲線
存在3條直線與曲線 相切,求t的取值范圍;
相切,求t的取值范圍;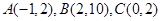 分別存在幾條直線與曲線
分別存在幾條直線與曲線 相切?(只需寫出結(jié)論)
相切?(只需寫出結(jié)論)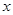 ,再代入原函數(shù)解析式,最后比較大小,即可;(2)設(shè)切點,由相切得出切線方程,然后列表并討論求出結(jié)果;(3)由(2)容易得出結(jié)果.
,再代入原函數(shù)解析式,最后比較大小,即可;(2)設(shè)切點,由相切得出切線方程,然后列表并討論求出結(jié)果;(3)由(2)容易得出結(jié)果.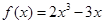 得
得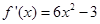 ,令
,令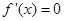 ,得
,得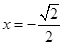 或
或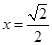 ,
,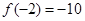 ,
,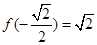 ,
,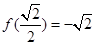 ,
,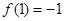 ,
,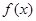 在區(qū)間
在區(qū)間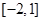 上的最大值為
上的最大值為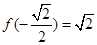 .
. 相切于點
相切于點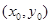 ,則
,則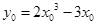 ,且切線斜率為
,且切線斜率為 ,所以切線方程為
,所以切線方程為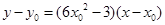 ,
,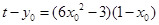 ,整理得:
,整理得: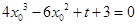 ,
,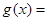
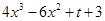 ,則“過點
,則“過點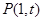 存在3條直線與曲線
存在3條直線與曲線 相切”等價于“
相切”等價于“ 有3個不同零點”,
有3個不同零點”, 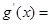
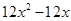 =
=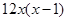 ,
, 與
與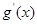 的情況如下:
的情況如下: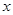 | 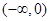 | 0 | 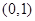 | 1 | 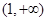 |
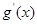 | + | 0 | 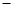 | 0 | + |
 |  | t+3 |  | 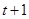 |  |
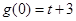 是
是 的極大值,
的極大值,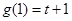 是
是 的極小值,
的極小值,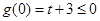 ,即
,即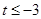 時,此時
時,此時 在區(qū)間
在區(qū)間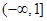 和
和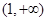 上分別至多有1個零點,所以
上分別至多有1個零點,所以 至多有2個零點,
至多有2個零點,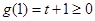 ,
,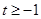 時,此時
時,此時 在區(qū)間
在區(qū)間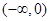 和
和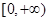 上分別至多有1個零點,所以
上分別至多有1個零點,所以 至多有2個零點.
至多有2個零點.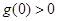 且
且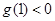 ,即
,即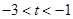 時,因為
時,因為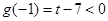 ,
,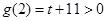 ,
, 分別為區(qū)間
分別為區(qū)間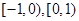 和
和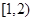 上恰有1個零點,由于
上恰有1個零點,由于 在區(qū)間
在區(qū)間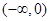 和
和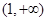 上單調(diào),所以
上單調(diào),所以 分別在區(qū)間
分別在區(qū)間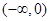 和
和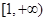 上恰有1個零點.
上恰有1個零點.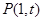 存在3條直線與曲線
存在3條直線與曲線 相切時,t的取值范圍是
相切時,t的取值范圍是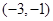 .
. 相切;
相切; 相切;
相切; 相切.
相切.

科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
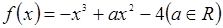 .
.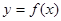 的圖象在點
的圖象在點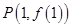 處的切線的傾斜角為
處的切線的傾斜角為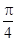 ,求
,求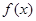 在
在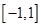 上的最小值;
上的最小值;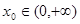 ,使
,使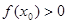 ,求a的取值范圍.
,求a的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.f(x1)<f(x2) | B.f(x1)=f(x2) |
| C.f(x1)>f(x2) | D.不確定 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com