
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),其中
為參數(shù)),其中![]() 為直線
為直線![]() 的傾斜角.以坐標(biāo)原點(diǎn)為極點(diǎn),以
的傾斜角.以坐標(biāo)原點(diǎn)為極點(diǎn),以![]() 軸的正半軸為極軸,建立極坐標(biāo)系,曲線
軸的正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若點(diǎn)![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,直線
,直線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() 且與曲線
且與曲線![]() 相交于
相交于![]() 兩點(diǎn),求
兩點(diǎn),求![]() 兩點(diǎn)間的距離
兩點(diǎn)間的距離![]() 的值.
的值.
【答案】(1)![]() ,C:
,C:![]() ;(2)8
;(2)8
【解析】
(1)用消參法可得直線的普通方程,由公式![]() 可化曲線
可化曲線![]() 的極坐標(biāo)方程為直角坐標(biāo)方程;
的極坐標(biāo)方程為直角坐標(biāo)方程;
(2)點(diǎn)![]() 的坐標(biāo)化為直角坐標(biāo),寫出直線的標(biāo)準(zhǔn)參數(shù)方程
的坐標(biāo)化為直角坐標(biāo),寫出直線的標(biāo)準(zhǔn)參數(shù)方程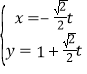 (
(![]() 為參數(shù)),代入曲線C的直角坐標(biāo)方程,應(yīng)用韋達(dá)定理,再由公式
為參數(shù)),代入曲線C的直角坐標(biāo)方程,應(yīng)用韋達(dá)定理,再由公式![]() 得弦長.
得弦長.
(1)消去參數(shù)![]() 得:
得:![]() ; 曲線C的方程化為
; 曲線C的方程化為![]() ,直角坐標(biāo)方程為
,直角坐標(biāo)方程為![]() ;
;
(2)∵點(diǎn)![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,∴點(diǎn)
,∴點(diǎn)![]() 的直角坐標(biāo)為
的直角坐標(biāo)為![]() .
.
∴![]() ,直線
,直線![]() 的傾斜角
的傾斜角![]() .∴直線
.∴直線![]() 的參數(shù)為
的參數(shù)為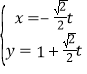 (
(![]() 為參數(shù)).
為參數(shù)).
代入![]() ,得
,得![]() .
.
設(shè)![]() 兩點(diǎn)對應(yīng)的參數(shù)為
兩點(diǎn)對應(yīng)的參數(shù)為![]() ,則
,則![]()
∴![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個不透明的袋子中有大小形狀完全相同的![]() 個乒乓球,乒乓球上分別印有數(shù)字
個乒乓球,乒乓球上分別印有數(shù)字![]() ,小明和小芳分別從袋子中摸出一個球(不放回),看誰摸出來的球上的數(shù)字大.小明先摸出一球說:“我不能肯定我們兩人的球上誰的數(shù)字大.”然后小芳摸出一球說:“我也不能肯定我們兩人的球上誰的數(shù)字大.”那么小芳摸出來的球上的數(shù)字是______.
,小明和小芳分別從袋子中摸出一個球(不放回),看誰摸出來的球上的數(shù)字大.小明先摸出一球說:“我不能肯定我們兩人的球上誰的數(shù)字大.”然后小芳摸出一球說:“我也不能肯定我們兩人的球上誰的數(shù)字大.”那么小芳摸出來的球上的數(shù)字是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)n為正整數(shù)集合![]() ,n對于集合A中的任意元素
,n對于集合A中的任意元素![]() 和
和![]() ,記
,記![]() .
.
(1)當(dāng)![]() 時,若
時,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)當(dāng)![]() 時,設(shè)B是A的子集,且滿足:對于B中的任意元素α,β,當(dāng)α,β相同時,
時,設(shè)B是A的子集,且滿足:對于B中的任意元素α,β,當(dāng)α,β相同時,![]() 是奇數(shù);當(dāng)α,β不同時,
是奇數(shù);當(dāng)α,β不同時,![]() 是偶數(shù).求集合B中元素個數(shù)的最值.
是偶數(shù).求集合B中元素個數(shù)的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù),![]() 其中
其中![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(Ⅰ)討論函數(shù)![]() 的單調(diào)性及極值;
的單調(diào)性及極值;
(Ⅱ)若不等式![]() 在
在![]() 內(nèi)恒成立,求證:
內(nèi)恒成立,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() .
.
(1)當(dāng)![]() 時,若函數(shù)
時,若函數(shù)![]() 存在與直線
存在與直線![]() 平行的切線,求實(shí)數(shù)
平行的切線,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時,
時,![]() ,若
,若![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩位學(xué)生參加數(shù)學(xué)競賽培訓(xùn),現(xiàn)分別從他們在培訓(xùn)期間參加的若干次預(yù)賽成績中隨機(jī)抽取8次,記錄如下:
甲:82,81,79,78,95,88,93,84
乙:92,95,80,75,83,80,90,85
(1)用莖葉圖表示這兩組數(shù)據(jù);
(2)現(xiàn)要從中選派一人參加數(shù)學(xué)競賽,從統(tǒng)計學(xué)的角度(在平均數(shù)、方差或標(biāo)準(zhǔn)差中選兩個)考慮,你認(rèn)為選派哪位學(xué)生參加合適?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】麻團(tuán)又叫煎堆,呈球形,華北地區(qū)稱麻團(tuán),是一種古老的中華傳統(tǒng)特色油炸面食,寓意團(tuán)圓。制作時以糯米粉團(tuán)炸起,加上芝麻而制成,有些包麻茸、豆沙等餡料,有些沒有。一個長方體形狀的紙盒中恰好放入4個球形的麻團(tuán),它們彼此相切,同時與長方體紙盒上下底和側(cè)面均相切,其俯視圖如圖所示,若長方體紙盒的表面積為576 ![]() ,則一個麻團(tuán)的體積為_______
,則一個麻團(tuán)的體積為_______![]() .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知右焦點(diǎn)為![]() 的橢圓
的橢圓![]() 關(guān)于直線
關(guān)于直線![]() 對稱的圖形過坐標(biāo)原點(diǎn).
對稱的圖形過坐標(biāo)原點(diǎn).
![]() 是橢圓
是橢圓![]() 的左頂點(diǎn),斜率為
的左頂點(diǎn),斜率為![]() 的直線交
的直線交![]() 于
于![]() ,
,![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 在
在![]() 上,
上,![]() .
.
(Ⅰ)當(dāng)![]() 時,求
時,求![]() 的面積;
的面積;
(Ⅱ)當(dāng)![]() 時,證明:
時,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】被嘉定著名學(xué)者錢大昕贊譽(yù)為“國朝算學(xué)第一”的清朝數(shù)學(xué)家梅文鼎曾創(chuàng)造出一類“方燈體”,“燈者立方去其八角也”,如圖所示,在棱長為![]() 的正方體
的正方體![]() 中,點(diǎn)
中,點(diǎn)![]() 為棱上的四等分點(diǎn).
為棱上的四等分點(diǎn).

(1)求該方燈體的體積;
(2)求直線![]() 和
和![]() 的所成角;
的所成角;
(3)求直線![]() 和平面
和平面![]() 的所成角.
的所成角.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com