
【題目】計算題
(1)已知cos( ![]() +x)=
+x)= ![]() ,(
,( ![]() <x<
<x< ![]() ),求
),求 ![]() 的值.
的值.
(2)若 ![]() ,
, ![]() 是夾角60°的兩個單位向量,求
是夾角60°的兩個單位向量,求 ![]() =2
=2 ![]() +
+ ![]() 與
與 ![]() =﹣3
=﹣3 ![]() +2
+2 ![]() 的夾角.
的夾角.
【答案】
(1)解:∵ ![]() <x<
<x< ![]() ,∴x+
,∴x+ ![]() ∈(
∈( ![]() ,2π),再結合cos(
,2π),再結合cos( ![]() +x)=
+x)= ![]() >0,可得sin(x+
>0,可得sin(x+ ![]() )=﹣
)=﹣ ![]() ,∴tan(x+
,∴tan(x+ ![]() )=﹣
)=﹣ ![]() .
.
由 ![]() (cosα﹣sinα)=
(cosα﹣sinα)= ![]() ,
, ![]() (sinα+cosα)=﹣
(sinα+cosα)=﹣ ![]() ,解得sinα=
,解得sinα= ![]() ,cosα=﹣
,cosα=﹣ ![]() ,tanα=9.
,tanα=9.
![]() =
= ![]() =﹣
=﹣ ![]()
(2)解: ![]() ,
, ![]() 是夾角60°的兩個單位向量,
是夾角60°的兩個單位向量, ![]() =2
=2 ![]() +
+ ![]() 與
與 ![]() =﹣3
=﹣3 ![]() +2
+2 ![]() ,
,
可得cos ![]() =
= ![]() =
= 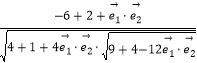 =
= ![]() =
= ![]() .
.
![]() =2
=2 ![]() +
+ ![]() 與
與 ![]() =﹣3
=﹣3 ![]() +2
+2 ![]() 的夾角為:120°
的夾角為:120°
【解析】(1.)由條件利用同角三角函數的基本關系求得 sin(x+ ![]() )的值,可得tan(x+
)的值,可得tan(x+ ![]() )的值,求出正弦函數與余弦函數值,即可求表達式的值. (2.)利用向量的數量積公式以及向量的模的運算法則化簡求解即可.
)的值,求出正弦函數與余弦函數值,即可求表達式的值. (2.)利用向量的數量積公式以及向量的模的運算法則化簡求解即可.
【考點精析】本題主要考查了數量積表示兩個向量的夾角的相關知識點,需要掌握設![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 與
與![]() 的夾角,則
的夾角,則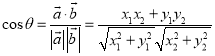 才能正確解答此題.
才能正確解答此題.


 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 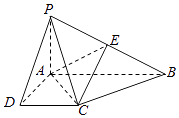
(1)求證:平面PAD⊥平面PCD;
(2)試在棱PB上確定一點E,使截面AEC把該幾何體分成的兩部分PDCEA與EACB的體積比為2:1;
(3)在(2)的條件下,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盒中共有形狀大小完全相同的5個球,其中有2個紅球和3個白球.若從中隨機取2個球,則概率為 ![]() 的事件是( )
的事件是( )
A.都不是紅球
B.恰有1個紅球
C.至少有1個紅球
D.至多有1個紅球
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定義域和值域均是[1,a],求實數a的值;
(2)若對任意的x1 , x2∈[1,a+1],總有|f(x1)﹣f(x2)|≤4,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設x,y滿足不等式組  ,若z=ax+y的最大值為2a+4,最小值為a+1,則實數a的取值范圍為( )
,若z=ax+y的最大值為2a+4,最小值為a+1,則實數a的取值范圍為( )
A.[﹣1,2]
B.[﹣2,1]
C.[﹣3,﹣2]
D.[﹣3,1]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)如圖,四面體ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
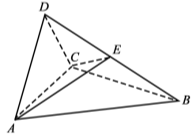
(1)證明:平面ACD⊥平面ABC;
(2)過AC的平面交BD于點E,若平面AEC把四面體ABCD分成體積相等的兩部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,AB= ![]() ,BC=1,E為線段DC上一動點,現將△AED沿AE折起,使點D在面ABC上的射影K在直線AE上,當E從D運動到C,則K所形成軌跡的長度為( )
,BC=1,E為線段DC上一動點,現將△AED沿AE折起,使點D在面ABC上的射影K在直線AE上,當E從D運動到C,則K所形成軌跡的長度為( ) 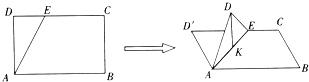
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com