
【題目】已知函數f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定義域和值域均是[1,a],求實數a的值;
(2)若對任意的x1 , x2∈[1,a+1],總有|f(x1)﹣f(x2)|≤4,求實數a的取值范圍.
【答案】
(1)解:∵f(x)=(x﹣a)2+5﹣a2(a>1),
∴f(x)在[1,a]上是減函數,又定義域和值域均為[1,a],
∴ ![]() ,
,
即 ![]() ,解得a=2
,解得a=2
(2)解:若a≥2,又x=a∈[1,a+1],且,(a+1)﹣a≤a﹣1
∴f(x)max=f(1)=6﹣2a,f(x)min=f(a)=5﹣a2.
∵對任意的x1,x2∈[1,a+1],總有|f(x1)﹣f(x2)|≤4,
∴f(x)max﹣f(x)min≤4,即(6﹣2a)﹣(5﹣a2)≤4,解得﹣1≤a≤3,
又a≥2,∴2≤a≤3.
若1<a<2,fmax(x)=f(a+1)=6﹣a2,f(x)min=f(a)=5﹣a2,
f(x)max﹣f(x)min≤4顯然成立,綜上1<a≤3
【解析】(1)先將函數進行配方得到對稱軸,判定出函數f(x)在[1,a]上的單調性,然后根據定義域和值域均為[1,a]建立方程組,解之即可;(2)將a與2進行比較,將條件“對任意的x1 , x2∈[1,a+1],總有|f(x1)﹣f(x2)|≤4”轉化成對任意的x1 , x2∈[1,a+1],總有f(x)max﹣f(x)min≤4恒成立即可.
【考點精析】利用函數的定義域及其求法和函數的值域對題目進行判斷即可得到答案,需要熟知求函數的定義域時,一般遵循以下原則:①![]() 是整式時,定義域是全體實數;②
是整式時,定義域是全體實數;②![]() 是分式函數時,定義域是使分母不為零的一切實數;③
是分式函數時,定義域是使分母不為零的一切實數;③![]() 是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零;求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的.
是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零;求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】若一個四棱錐底面為正方形,頂點在底面的射影為正方形的中心,且該四棱錐的體積為9,當其外接球表面積最小時,它的高為( )
A.3
B.2 ![]()
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知矩形ABCD中,AB=2,AD=1,M為CD的中點.如圖將△ADM沿AM折起,使得平面ADM⊥平面ABCM. 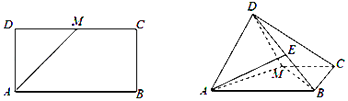
(1)求證:BM⊥平面ADM;
(2)若點E是線段DB上的中點,求三棱錐E﹣ABM的體積V1與四棱錐D﹣ABCM的體積V2之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】龍虎山花語世界位于龍虎山主景區排衙峰下,是一座獨具現代園藝風格的花卉公園,園內匯集了![]() 余種花卉苗木,一年四季姹紫嫣紅花香四溢.花園景觀融合法、英、意、美、日、中六大經典園林風格,景觀設計唯美新穎,玫瑰花園、香草花溪、臺地花海、植物迷宮、兒童樂園等景點錯落有致,交相呼應又自成一體,是世界園藝景觀的大展示.該景區自
余種花卉苗木,一年四季姹紫嫣紅花香四溢.花園景觀融合法、英、意、美、日、中六大經典園林風格,景觀設計唯美新穎,玫瑰花園、香草花溪、臺地花海、植物迷宮、兒童樂園等景點錯落有致,交相呼應又自成一體,是世界園藝景觀的大展示.該景區自![]() 年春建成,試運行以來,每天游人如織,郁金香、向日葵、虞美人等賞花旺季日入園人數最高達萬人.
年春建成,試運行以來,每天游人如織,郁金香、向日葵、虞美人等賞花旺季日入園人數最高達萬人.
某學校社團為了解進園旅客的具體情形以及采集旅客對園區的建議,特別在![]() 年
年![]() 月
月![]() 日賞花旺季對進園游客進行取樣調查,從當日
日賞花旺季對進園游客進行取樣調查,從當日![]() 名游客中抽取
名游客中抽取![]() 人進行統計分析,結果如下:
人進行統計分析,結果如下:
年齡 | 頻數 | 頻率 | 男 | 女 |
|
|
|
|
|
| ① | ② | ③ | ④ |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合計 |
|
|
|
|
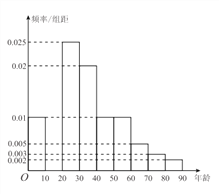
(I)完成表一中的空位①~④,并作答題紙中補全頻率分布直方圖,并估計![]() 年
年![]() 月
月![]() 日當日接待游客中
日當日接待游客中![]() 歲以下的游戲的人數.
歲以下的游戲的人數.
(II)完成表二,并判斷能否有![]() 的把握認為在觀花游客中“年齡達到
的把握認為在觀花游客中“年齡達到![]() 歲以上”與“性別”相關;
歲以上”與“性別”相關;
(表二)
|
| 合計 | |
男生 | |||
女生 | |||
合計 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式: 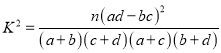 ,其中
,其中![]() )
)
(III)按分層抽樣(分![]() 歲以上與
歲以上與![]() 歲以下兩層)抽取被調查的
歲以下兩層)抽取被調查的![]() 位游客中的
位游客中的![]() 人作為幸運游客免費領取龍虎山內部景區門票,再從這
人作為幸運游客免費領取龍虎山內部景區門票,再從這![]() 人中選取
人中選取![]() 人接受電視臺采訪,設這
人接受電視臺采訪,設這![]() 人中年齡在
人中年齡在![]() 歲以上(含
歲以上(含![]() 歲)的人數為
歲)的人數為![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定義域為R的奇函數.
(1)求k值;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值為﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值為﹣2,求m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某項體育比賽中,七位裁判為一選手打出的分數如下: 90 89 90 95 93 94 93
去掉一個最高分和一個最低分后,所剩數的平均值和方差分別為( )
A.92,2
B.92,2.8
C.93,2
D.93,2.8
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計算題
(1)已知cos( ![]() +x)=
+x)= ![]() ,(
,( ![]() <x<
<x< ![]() ),求
),求 ![]() 的值.
的值.
(2)若 ![]() ,
, ![]() 是夾角60°的兩個單位向量,求
是夾角60°的兩個單位向量,求 ![]() =2
=2 ![]() +
+ ![]() 與
與 ![]() =﹣3
=﹣3 ![]() +2
+2 ![]() 的夾角.
的夾角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}、{bn}滿足:a1= ![]() ,an+bn=1,bn+1=
,an+bn=1,bn+1= ![]() .
.
(1)求a2 , a3;
(2)證數列{ ![]() }為等差數列,并求數列{an}和{bn}的通項公式;
}為等差數列,并求數列{an}和{bn}的通項公式;
(3)設Sn=a1a2+a2a3+a3a4+…+anan+1 , 求實數λ為何值時4λSn<bn恒成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=sin(ωx+φ)(ω>0,|φ|< ![]() )在同一個周期內,當x=
)在同一個周期內,當x= ![]() 時y取最大值1,當x=
時y取最大值1,當x= ![]() 時y取最小值﹣1.
時y取最小值﹣1.
(1)求函數的解析式y=f(x);
(2)當x∈[ ![]() ,
, ![]() ]時.求函數y=f(x)的值域.
]時.求函數y=f(x)的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com